sLecture

↳ Topic 1: Optical Imaging Systems

↳ Intro

↳ Lenses

↳ Space Domain Models for Optical Imaging Systems

Excerpt from Prof. Bouman's Lecture

Accompanying Lecture Notes

Some Basic Properties and Assumptions

First let's review some basics about lenses. For these notes, we will discuss lenses assuming the thin lens model (i.e. assume that the thickness of the lens is negligible compared to its focal length).

A Biconvex Lens

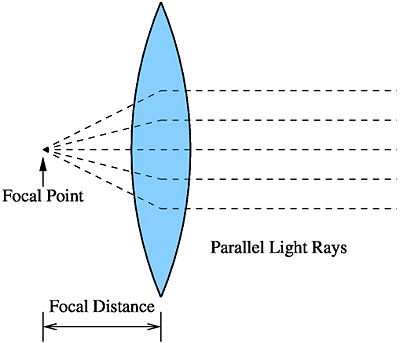
When parallel light rays are incident upon a biconvex lens, they converge at one point after passing through. This point is called the focal point of the lens. The distance from the optical center of the lens to the focal point is called the focal distance or focal length.

Note that the focal distance can be different for the two sides of the lens if the lens is not perfectly symmetric.

We can approximate light rays from the sun to be parallel but ideally, for a source to produce perfectly parallel light rays, it would have to be an infinite distance away from your lens.

Image Formation

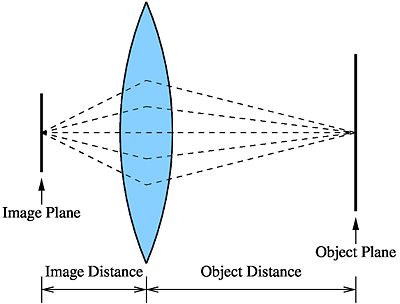
Most of your photography subjects however, will not be an infinite distance away. In that case your object's distance from the lens is some finite quantity and the image plane has to be adjusted so that the image is in focus.

Image Formation via a Biconvex Lens

Let $ d_f $ be the focal length of the lens. This quantity is an intrinsic property of the lens.

Let $ d_o $ be the distance of the object plane from the optical center of the lens.

Let $ d_i $ be the distance of the image plane from the optical center of the lens.

So for your image to be in focus, the following equation must be satisfied.

$ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{d_f} $

Notice that

$ \begin{align} d_o &= \infty \\ \Rightarrow \frac{1}{d_i} &= \frac{1}{d_f} \\ \Rightarrow d_i &= d_f \end{align} $

which is what we stated earlier when defining focal length.

Also note that

$ d_i = (\frac{1}{d_f} - \frac{1}{d_o})^{-1} $

So the smaller the $ d_o $, the smaller the reciprocal of $ d_i $ and hence the larger $ d_i $ is. In other words, as the object plane moves in, the image plane moves out.

Magnification

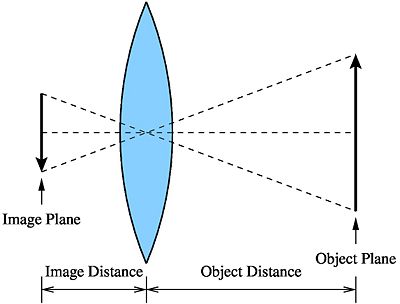
Typically, when you view an image through a lens, there is an effective magnification.

Magnification and Inversion of an Image through a Biconvex Lens

Let $ M $ be the magnification factor of the lens.

For a biconvex lens,

$ M = -\frac{d_i}{d_o} $

The negative sign denotes that for a biconvex lens, the image is also inverted. This phenomena is also illustrated in the above figure.

Normally, the image you form using your camera is much smaller than the actual object. In other words, $ |M| < 1 $. So in a typical camera, we have that

$ d_o >> d_f \ $

$ \Rightarrow d_i = \frac{d_o d_f}{d_o - d_f} \approx d_f $

Additionally, if $ d_i > d_f $, then $ |M| << 1 $.

However, when the object is closer to the lens than its focal length, $ |M| > 1 $ and the image is larger than the object. This is the principle used in microscopes to magnify (in absolute terms) objects.

$ d_i >> d_f \ $

$ \Rightarrow d_o = \frac{d_i d_f}{d_i - d_f} \approx d_f $

Additionally, if $ d_o > d_f $, then $ |M| >> 1 $.

Aperture and f-Stop

The effective size of the lens is controlled by the aperture of your camera. The aperture is like the pupil of your eye. The iris contracts and dilates the pupil when you are in a bright or dark environment. Similarly you may want to limit the amount of light entering the camera to stay within the dynamic range of the sensors.

Aperture of a Lens

Let $ A $ be the diameter of the aperture.

Let $ d_f $ be the focal distance of the lens.

Let $ N $ be the f-stop of the lens.

Then,

$ N := \frac{d_f}{A} $

Also the area of the aperture is given by

If $ N $ is large, then A is small, meaning that less light enters the lens. You may have to leave your aperture open for longer to get a bright picture but this also increases the chances of blurriness unless your subject is very still throughout the exposure. The lens is often described to be slow.

If, on the other hand, N is small, A is large. You have lots of light coming in at once so you need a faster shutter speed (a faster lens). This design is generally more expensive and is handy when you are doing sport photography.

Since light is proportional to the area of the aperture,

$ Light \propto Area = \frac{\pi A^{2}}{4} = \frac{\pi}{4}(\frac{d_f}{N})^{2} = \frac{\pi d_f}{4}\frac{1}{N^{2}} $

So we see that light is inversely proportional to the square of $ N $. Theoretically, the larger the aperture, the sharper the image. However, this is not always true in practice.

There are two reasons why constraining the aperture can improve the quality of an image:

• light rays that are incident close to the edges of the lens produce effects such as barrel distortion. You wan to reduce the aperture so that light is incident close to the lens's center.
• as the lens gets larger, the depth of field becomes smaller.

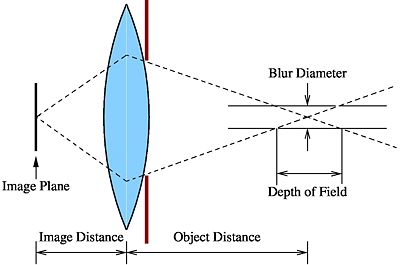
Depth of Field

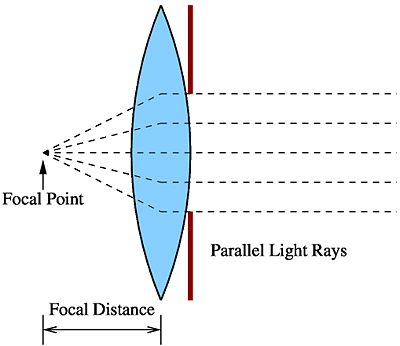
The figures below shows a biconvex lens and the depth of filed for the different apertures. Notice that for a wider aperture, you would get a sharper image on the image plane corresponding to a narrower point spread function in the (x,y) domain. But for a fixed blur diameter, the depth of field would be much shallower.

Depth of Field of a Biconvex Lens

Depth of Field of a Biconvex Lens Smaller Aperture

Let $ D $ be the depth of filed.

Let $ C_o $ be the blur diameter.

$ N $ and $ M $ are as defined previously.

Then we have the following relationship

$ \begin{align} \frac{D}{C_0} &= -\frac{2N}{M} \\ \Rightarrow D &= -\frac{2M C_0}{N} \end{align} $

This relationship reiterates what we saw in the diagrams that if you fix $ C_0 $ then $ D $ is directly proportional to $ N $. Equivalently, $ D $ is inversely proportional to $ A $.

If you were at the Leaning Tower of Pisa and you wanted to take that picture of yourself propping the tower up, you would want a camera with a large depth of field because otherwise the tower would show up very blurry in your photo. But a shallow depth of field can also be useful. Cinematographers may use a camera with shallow depth of field to blur the foreground and background to isolate a subject and make it stand out to viewers.

References

• C. A. Bouman. ECE 637. Class Lecture. Digital Image Processing I. Faculty of Electrical Engineering, Purdue University. Spring 2013.

Questions and comments

If you have any questions, comments, etc. please post them on this page

Back to the "Bouman Lectures on Image Processing" by Maliha Hossain