7.11 QE 2006 January
1 (33 points)
Let $ \mathbf{X} $ and $ \mathbf{Y} $ be two joinly distributed random variables having joint pdf
$ f_{\mathbf{XY}}\left(x,y\right)=\left\{ \begin{array}{lll} 1, & & \text{ for }0\leq x\leq1\text{ and }0\leq y\leq1\\ 0, & & \text{ elsewhere. } \end{array}\right. $
(a)
Are $ \mathbf{X} $ and $ \mathbf{Y} $ statistically independent? Justify your answer.
$ f_{\mathbf{X}}\left(x\right)=\int_{-\infty}^{\infty}f_{\mathbf{XY}}\left(x,y\right)dy=\int_{0}^{1}dy=1\text{ for }0\leq x\leq1. $
$ f_{\mathbf{Y}}\left(y\right)=\int_{-\infty}^{\infty}f_{\mathbf{XY}}\left(x,y\right)dx=\int_{0}^{1}dx=1\text{ for }0\leq y\leq1. $
Since $ f_{\mathbf{XY}}\left(x,y\right)=f_{\mathbf{X}}\left(x\right)f_{\mathbf{Y}}\left(y\right) $ , $ \mathbf{X} $ and $ \mathbf{Y} $ are $ statistically independent. $
(b)
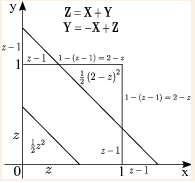
Let $ \mathbf{Z} $ be a new random variable defined as $ \mathbf{Z}=\mathbf{X}+\mathbf{Y} $ . Find the cdf of $ \mathbf{Z} $ .
$ F_{\mathbf{Z}}\left(z\right)=P\left(\left\{ \mathbf{Z}\leq z\right\} \right)=P\left(\left\{ \mathbf{X}+\mathbf{Y}\leq z\right\} \right). $
• i) if $ z<0 $ , then $ F_{\mathbf{Z}}\left(z\right)=0 $ .
• ii) if $ z\geq2 $ , then $ F_{\mathbf{Z}}\left(z\right)=1 $ .
• iii) if $ 0\leq z\leq1 $ , then $ F_{\mathbf{Z}}\left(z\right)=\iint f_{\mathbf{XY}}\left(x,y\right)dxdy=\iint1\cdot dxdy=\frac{1}{2}z^{2} $ .
• iv) if $ 1<z<2 $ , then $ F_{\mathbf{Z}}=\iint f_{\mathbf{XY}}\left(x,y\right)dxdy=\iint1\cdot dxdy=1-\frac{1}{2}\left(2-z\right)^{2} $ .
$ \therefore F_{\mathbf{Z}}\left(z\right)=\left\{ \begin{array}{lll} 0 & & ,z<0\\ \frac{1}{2}z^{2} & & ,0\leq z\leq1\\ 1-\frac{1}{2}\left(2-z\right)^{2} & & ,1<z<2\\ 1 & & ,z\geq2 \end{array}\right. $
(c)
Find the variance of $ \mathbf{Z} $ .
$ f_{\mathbf{Z}}\left(z\right)=\left\{ \begin{array}{lll} z & & ,0\leq z\leq1\\ 2-z & & ,1<z<2\\ 0 & & \text{,otherwise.} \end{array}\right. $
$ E\left[\mathbf{Z}\right]=\int_{-\infty}^{\infty}z\cdot f_{\mathbf{Z}}\left(z\right)dz=\int_{0}^{1}z^{2}dz+\int_{1}^{2}\left(2z-z^{2}\right)dz=\frac{1}{3}z^{3}\Bigl|_{0}^{1}+z^{2}-\frac{1}{3}z^{3}\Bigl|_{1}^{2}=\frac{1}{3}+3-\frac{7}{3}=1. $ $ E\left[\mathbf{Z}^{2}\right]=\int_{-\infty}^{\infty}z^{2}\cdot f_{\mathbf{Z}}\left(z\right)dz=\int_{0}^{1}z^{3}dz+\int_{1}^{2}\left(2z^{2}-z^{3}\right)dz=\frac{1}{4}z^{4}\Bigl|_{0}^{1}+\frac{2}{3}z^{3}-\frac{1}{4}z^{4}\Bigl|_{1}^{2}=\frac{1}{4}+\frac{14}{3}-\frac{15}{4}=\frac{7}{6}. $ $ Var\left[\mathbf{Z}\right]=E\left[\mathbf{Z}^{2}\right]-\left(E\left[\mathbf{Z}\right]\right)^{2}=\frac{1}{6}. $
2 (33 points)
Suppose that $ \mathbf{X} $ and $ \mathbf{N} $ are two jointly distributed random variables, with $ \mathbf{X} $ being a continuous random variable that is uniformly distributed on the interval $ \left(0,1\right) $ and $ \mathbf{N} $ being a discrete random variable taking on values $ 0,1,2,\cdots $ and having conditional probability mass function $ p_{\mathbf{N}}\left(n|\left\{ \mathbf{X}=x\right\} \right)=x^{n}\left(1-x\right),\quad n=0,1,2,\cdots $ .
(a)
Find the probability that \mathbf{N}=n .
$ f_{\mathbf{X}}\left(x\right)=\left\{ \begin{array}{lll} 1 & & ,0\leq x\leq1\\ 0 & & ,\text{otherwise.} \end{array}\right. $
$ P\left(\left\{ \mathbf{N}=n\right\} \right)=\int_{-\infty}^{\infty}p_{\mathbf{N}}\left(n|\left\{ \mathbf{X}=x\right\} \right)f_{\mathbf{X}}\left(x\right)dx=\int_{0}^{1}x^{n}\left(1-x\right)dx $
$ =\frac{1}{n+1}x^{n+1}-\frac{1}{n+2}x^{n+2}\Bigl|_{0}^{1}=\frac{1}{n+1}-\frac{1}{n+2}=\frac{1}{\left(n+1\right)\left(n+2\right)}. $
(b)
Find the conditional density of $ \mathbf{X} $ given $ \left\{ \mathbf{N}=n\right\} $ .
By using Bayes' theorem,
$ f_{\mathbf{X}}\left(x|\left\{ \mathbf{N}=n\right\} \right)=\frac{p_{\mathbf{N}}\left(n|\left\{ \mathbf{X}=x\right\} \right)f_{\mathbf{X}}\left(x\right)}{p_{\mathbf{N}}\left(n\right)}=\left\{ \begin{array}{lll} \left(n+1\right)\left(n+2\right)x^{n}\left(1-x\right) & & ,0\leq x\leq1\\ 0 & & ,\text{otherwise.} \end{array}\right. $
(c)
Find the minimum mean-square error estimator of $ \mathbf{X} $ given $ \left\{ \mathbf{N}=n\right\} $ .
$ MMSE=E\left[\mathbf{X}|\left\{ \mathbf{N}=n\right\} \right]=\int_{-\infty}^{\infty}x\cdot f_{\mathbf{X}}\left(x|\left\{ \mathbf{N}=n\right\} \right)dx=\int_{0}^{1}\left(n+1\right)\left(n+2\right)x^{n+1}\left(1-x\right)dx $$ =\left(n+1\right)\left(n+2\right)\left(\frac{1}{n+2}x^{n+2}-\frac{1}{n+3}x^{n+3}\right)\biggl|_{0}^{1}=\left(n+1\right)\left(n+2\right)\left(\frac{1}{n+2}-\frac{1}{n+3}\right) $$ =\frac{\left(n+1\right)\left(n+2\right)}{\left(n+2\right)\left(n+3\right)}=\frac{n+1}{n+3}. $
3 (34 points)
Assume that the locations of cellular telephone towers can be accurately modeled by a 2-dimensional homogeneous Poisson process for which the following two facts are know to be true:
1. The number of towers in a region of area A is a Poisson random variable with mean \lambda A , where \lambda>0 .
2. The number of towers in any two disjoint regions are statistically independent.
Assume you are located at a point we will call the origin within this 2-dimensional region, and let $ R_{\left(1\right)}<R_{\left(2\right)}<R_{\left(3\right)}<\cdots $ be the ordered distances between the origin and the towers.
(a)
Show that $ R_{\left(1\right)}^{2},R_{\left(2\right)}^{2},R_{\left(3\right)}^{2},\cdots $ are the points of a one-dimensional homogeneous Poisson process.
$ P\left(R_{\left(k+1\right)}^{2}-R_{\left(k\right)}^{2}>r\right)=P\left(\text{there is no tower in area }\pi r\right)=\frac{\left(\lambda\pi r\right)^{0}}{0!}e^{-\lambda\pi r}=e^{-\lambda\pi r}. $
$ P\left(R_{\left(k+1\right)}^{2}-R_{\left(k\right)}^{2}\leq r\right)=P\left(\left\{ \text{there is at least one tower in area }\pi r\right\} \right) $$ =1-e^{-\lambda\pi r}\text{: CDF of exponential random variable}. $
ref. You can see the expressions about exponentail distribution [CS1ExponentialDistribution].
$ R_{\left(k+1\right)}^{2}-R_{\left(k\right)}^{2} $ is an exponential random variable with parameter $ \lambda\pi $ .
$ \therefore R_{\left(1\right)}^{2},R_{\left(2\right)}^{2},R_{\left(3\right)}^{2},\cdots $ are the points of a one-dimensional homogeneous Poisson process.
(b)
What is the rate of the Poisson process in part (a)? $ \lambda\pi $ .
cf. The mean value for the exponential random variable is $ \frac{1}{\lambda\pi} $ .
(c)
Determine the density function of $ R_{\left(k\right)} $ , the distance to the $ k $ -th nearest cell tower.
$ F_{k}\left(x\right)\triangleq P\left(R_{\left(k\right)}\leq x\right) $$ =P\left(\text{There are at least }k\text{ towers within the distance between origin and }x\right) $$ =P\left(N\left(0,x\right)\geq k\right)=1-P\left(N\left(0,x\right)\leq k-1\right)=1-\sum_{j=0}^{k-1}\frac{\left(\lambda\pi x^{2}\right)^{j}}{j!}e^{-\lambda\pi x^{2}}. $
$ f_{k}\left(x\right)=\frac{dF_{k}\left(x\right)}{dx}=-\sum_{j=0}^{k-1}\left\{ \frac{j\left(\lambda\pi x^{2}\right)^{j-1}\left(2\lambda\pi x\right)}{j!}e^{-\lambda\pi x^{2}}+\frac{\left(\lambda\pi x^{2}\right)^{j}}{j!}e^{-\lambda\pi x^{2}}\left(-2\lambda\pi x\right)\right\} $$ =\left(2\lambda\pi x\right)e^{-\lambda\pi x^{2}}\cdot\left\{ -\sum_{j=1}^{k-1}\frac{\left(\lambda\pi x^{2}\right)^{j-1}}{\left(j-1\right)!}e^{-\lambda\pi x^{2}}+\sum_{j=0}^{k-1}\frac{\left(\lambda\pi x^{2}\right)^{j}}{j!}\right\} $$ =\left(2\lambda\pi x\right)e^{-\lambda\pi x^{2}}\cdot\left\{ -\sum_{j=0}^{k-2}\frac{\left(\lambda\pi x^{2}\right)^{j}}{j!}+\sum_{j=0}^{k-1}\frac{\left(\lambda\pi x^{2}\right)^{j}}{j!}\right\} $$ =\left(2\lambda\pi x\right)e^{-\lambda\pi x^{2}}\cdot\frac{\left(\lambda\pi x^{2}\right)^{k-1}}{\left(k-1\right)!}. $
Back to the general ECE PHD QE page (for problem discussion)