Back to all ECE 600 notes

The Comer Lectures on Random Variables and Signals

Slectures by Maliha Hossain

Topic 18: Stochastic Convergence

Stochastic Convergence

We will now consider infinite sequences of random variables. We will discuss what it means for such a sequence to converge. This will lead to some very important results: the laws of large numbers and the Central Limit Theorem.

Consider a sequence X$ _1 $,X$ _2 $,..., where each X$ _i $ is a random variable on (S,F,P). We will call this a random sequence (or a discrete-time random process).

Notation $ \qquad $ X$ _n $ may refer to either the sequence itself or to the nth element in the sequence. We may also use {X$ _n $} to denote the sequence, or X$ _n $, n ≥ 1.

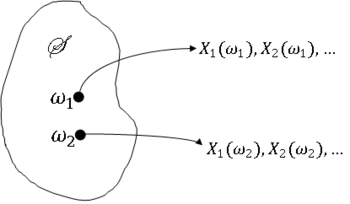
The sequence X$ _n $ maps S to the set of all sequences of real numbers, so for a fixed S, X$ _1(\omega) $,X$ _2(\omega) $,... is a sequence of real numbers.

Fig 1: The mapping from the sample space to the reals under X$ _j $.


Before looking at convergence, recall the meaning of convergence or a sequence of real numbers.

Definition $ \qquad $ A sequence of real numbers x$ _1 $,x$ _2 $,... converges to a number x ∈ R if ∀$ \epsilon $ > 0, ∃ an n$ _{\epsilon} $ ∈ N such that

$ |x_n-x|<\epsilon\qquad\forall n\geq n_{\epsilon} $

If there is such an x ∈ R, we say

$ \lim_{n\rightarrow\infty}x_n=x $

or

$ x_n\rightarrow\infty\;\mbox{as}\;n\rightarrow\infty $

For a random sequence X$ _n $, the issue of convergence is more complicated since X$ _n $ is a function of $ \omega $ ∈ S.

First look at a motivating example.

Example $ \qquad $ Let X$ _k $ = s + W$ _k $, where s ∈ R and W$ _k $ is a random sequence with E[W$ _k $] = 0 ∀k = 1,2,.... W$ _k $ can be viewed as a noise sequence if we want to know the value of s.

Let

$ Y_n=\frac{1}{n}\sum_{k=1}^nX_k $

Then, E[Y$ _n $] = s ∀n. But Y$ _n $ is a random variable, so we cannot expect Y$ _n $ = s ∀n. However, we intuitively expect Y$ _n $ to be a better estimate of s as n increases. Does Y$ _n $ → s as n → ∞ ? If so, in what sense?


Types of Convergence

Since X$ _n(\omega) $ is generally a different sequence for very $ \omega $ ∈ S, what does it mean for X$ _n $ to converge? We will discuss different ways in which X$ _n $ can converge.

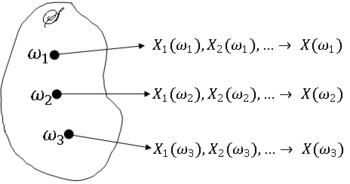
Definition $ \qquad $ X$ _n $ converges everywhere if the sequence X$ _1(\omega) $,X$ _2(\omega) $,... converges to some value X$ (\omega) $ ∀$ \omega $ ∈ S. We also call this sure convergence or convergence surely.


Fig 2: Convergence for all $ \omega $ in S.

Notation

$ X_n\overset{e}{\rightarrow}X $


Definition $ \qquad $ X$ _n $ converges almost everywhere or almost surely, if X$ _n(\omega) $ → X$ (\omega) $ for some A ∈ S with P(A) = 1. Also known as convergence with probability 1.

Notation

$ X_n\overset{a.e.}{\rightarrow}X,\quad X_n\overset{a.s.}{\rightarrow}X,\quad X_n\overset{w.p.1}{\rightarrow}X $


Definition $ \qquad $ X$ _n $ converges in mean square to X if

$ E\left[|X_n-X|^2\right]\rightarrow 0 $

as

$ n\rightarrow\infty $

Notation

$ X_n\overset{ms}{\rightarrow}X $


Definition X$ _n $ converges in probability to X if ∀$ \epsilon $ > 0

$ P(|X_n-X|>\epsilon)\rightarrow 0 $

as

$ n\rightarrow\infty $

Note that P(|X$ _n $ - X| > $ \epsilon $) is a sequence of real numbers.

Notation

$ X_n\overset{p}{\rightarrow}X $


Definition $ \qquad $ X$ _n $ converges in distribution to X if

$ F_{X_n}(x)\rightarrow F_X(x) $

as

$ n\rightarrow\infty $

Note that for a fixed x ∈ R, F$ _n $(x) is a sequence of real numbers.

Notation

$ X_n\overset{d}{\rightarrow}X $

We will generally assume that if X$ _n $ converges in distribution, then

$ \frac{F_{X_n}(x)}{dx}\rightarrow\frac{F_X(x)}{dx} $

or
$ f_{X_n}(x)\rightarrow f_X(x) $
as

$ n\rightarrow\infty $

although this is not true in every instance, as seen in the next example.

Example $ \qquad $ Let X$ _n $ have pdf

$ f_{X_n}(x) = 1+\cos 2\pi nx\quad0\leq x\leq 1,\;\;n=1,2,... $

Then

$ F_{X_n}(x) = \begin{cases} 0 & x<0 \\ x+\frac{\sin 2\pi nx}{2\pi n} & 0\leq x\leq 1 \\ 1 & x>1 \end{cases} $

Now

$ F_{X_n}(x)\rightarrow F_X(x) $

as
$ n\rightarrow\infty $

$ \forall x\in\mathbb R $

where

$ F_X(x)=\begin{cases} 0 & x<0 \\ x & 0\leq x\leq 1 \\ 1 & x>1 \end{cases} $

However, f$ _{Xn} $ does not converge for x ∈ (0,1).


Cauchy Criterion for Convergence

We will now discuss a method for showing that X$ _n $ → X in the mean square sense for some random variables X without knowing what X is. Frist, consider a sequence of real numbers.

Definition If x$ _n $ is a sequence of real numbers and

$ |x_{m+n}-x_n|\rightarrow 0 $

as

$ n\rightarrow \infty \quad \forall m>0 $

then x$ _n $ converges iff it is a Cauchy sequence. This is known as the Cauchy criterion for convergence.

The Cauchy Criterion for mean square convergence of X$ _n $ $ \qquad $ It can be shown that a random sequence X$ _n $ converges in the mean square sense iff

$ E[|X_{n+m}-X_n|^2]\rightarrow 0\quad\forall m>0 $

as

$ n\rightarrow\infty $

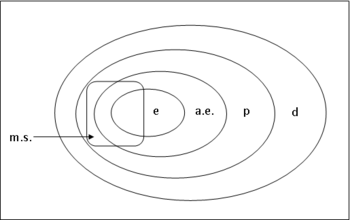
It can be shown that the following relationships between types of convergences hold:

Fig 3: Relationships implied by the different types of convergence. Note that the box represents all possible random sequences


Some Important Random Sequences

First, we need the Chebyshev Inequality:
Let X be a random variable with mean $ \mu $ and variance $ \sigma^2 $. Then,

$ P(|X_\mu|\geq\epsilon)\leq\frac{\sigma^2}{\epsilon^2}\quad\forall\epsilon>0 $

and

$ g_2(x) = \frac{(x-\mu)^2}{\epsilon^2} $

Proof $ \quad $ let

$ g_1(x) = I_{\{x\in\mathbb R:|x-\mu|\geq\epsilon\}}(x) $

for a fixed ε > 0. Then,

$ \begin{align} E[g_1(x)]&=\int_{-\infty}^{\infty}g_1(x)f_X(x)dx \\ &=P(|X-\mu|\geq\epsilon) \end{align} $

and

$ E[g_2(X)]=E\left[\frac{(X-\mu)^2}{\epsilon^2}\right]=\frac{\sigma^2}{\epsilon^2} $

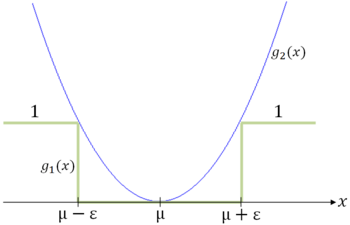
Now consider $ \phi $(x) = g$ _2 $(x) - g$ _1 $(x)

Fig 4: g$ _1 $ and g$ _2 $ as functions of x. Note that g$ _2 $(x) ≥ g$ _1 $(x) for all x.

We have that $ \phi $(x) ≥ 0 ∀x ∈ R. So,

$ 0\leq E[\phi(X)]=E[g_2(X)]-E[g_1(X)]=\frac{\sigma^2}{\epsilon^2}-P(|X-\mu|\geq\epsilon) $
$ \Rightarrow P(|X_\mu|\geq\epsilon)\leq\frac{\sigma^2}{\epsilon^2} $


The Laws of Large Numbers

Recall that the previous example where

$ X_k=s+W_k \ $

where s ∈ R and E[W$ _k $] = 0. Let

$ Y_n=\frac{1}{n}\sum_{k=1}^n X_k $

Does Y$ _n $ converge to s? If so, in what sense? The laws of large numbers address this question.

Theorem $ \qquad $ The Weak Law of Large Numbers
Let X$ _n $ be a sequence of iid random variables with mean $ \mu $ and variance $ \sigma^2 $. Let

$ Y_n=\frac{1}{n}\sum_{k=1}^n X_k $

Y$ _n $ is the sample mean.
Then, for any $ \epsilon $ < 0,

$ P(|Y_n-\mu|\geq\epsilon)\rightarrow0 $

as

$ n\rightarrow\infty $

i.e., Y$ _n $ → $ \mu $ in probability.

Proof

$ \begin{align} E[Y_n]&=\mu \\ \mbox{Var}(Y_n)&=\frac{\sigma^2}{n} \end{align} $

Using the Chebyshev Inequality, we have that

$ P(|Y_n-\mu|\geq\epsilon)\leq\frac{\mbox{Var}(Y_n)}{\epsilon^2}=\frac{\sigma^2}{\epsilon^2n}\;\overset{n\rightarrow\infty}{\longrightarrow}\;0 $

Theorem $ \qquad $ Strong Law of Large Numbers
Let X$ _n $ be a sequence of iid random variables with mean $ \mu $ and variance $ \sigma^2 $. Then

$ Y_n=\frac{1}{n}\sum_{k=1}^nX_k\overset{a.e.}{\longrightarrow}\mu $

as

$ n\rightarrow\infty $

The proof is omitted as it is beyond the scope of this class. Nevertheless, note that the strong law of large numbers implies the weak law of large numbers.

So for example

$ X_k=s+W_k \ $

if the W$ _k $'s are independent and have the same variance $ \sigma^2 $, then the sample mean Y$ _n $ converges to s with probability 1.

But the laws of large numbers tell us something more fundamental about our axiomatic-based probability measure. Consider a random variable X and a set A ⊂ B(R). Let X$ _1 $,X$ _2 $,... be an iid sequence of random variables with the same distribution as X. Now let

$ Y_k=\begin{cases} 1 & \mbox{if} \;X_k\in A \\ 0 & \mbox{if} \;X_k\notin A \end{cases} $

Then

$ E[Y_k] = P(X_k\in A) = P(X\in A) $

The Y $ _k $'s are iid with with mean P(X ∈ A) and the relative frequency of the even {X ∈ A} is

$ \frac{1}{n}\sum_{k=1}^nY_k $

The strong law pf large number tells us that

$ \frac{1}{n}\sum_{k=1}^nY_k\rightarrow P(X\in A) $

with probability 1 as

$ n\rightarrow\infty $

So with probability 1, the relative frequency approach to probability converges to the axiom-based P(X ∈ A).


The Central Limit Theorem

Let X$ _n $ be a sequence of iid random variables with finite mean $ \mu $ and variance $ \sigma^2 $. Then if

$ Z_n = \frac{\sum_{j=1}^nX_j-n\mu}{\sigma\sqrt{n}} $

then,

$ Z_n\overset{d}{\longrightarrow}Z $

as

$ n\rightarrow\infty $

where Z is N(0,1).

i.e.

$ F_{Z_n}(z)\rightarrow\Phi(z)=\int_{-\infty}^z\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx $

Proof $ \qquad $ We will use the following Lemma

Lemma $ \qquad $ Let Z$ _n $ be a sequence of random variables with cdfs F$ _{Zn} $ and mgfs $ \Phi_{Zn} $(s), and let Z be a random variable with cdf F$ _Z $ and mgf $ \Phi_Z $. Then if $ \Phi_{Zn} $(s) → $ \Phi_Z $ ∀s ∈ C, then F$ _{Zn} $(z) → F$ _Z $(z) ∀z ∈ R.

So it is sufficient to show that

$ \Phi_{Z_n}(s)\rightarrow e^{\frac{s^2}{2}} $

Consider

$ \Phi_X\left(\frac{s}{\sqrt n}\right)=E\left[e^{\frac{sX_k}{\sqrt n}}\right]\quad\forall k $

Now considering the case $ \mu=0 $, $ \sigma^2=1 $, we have

$ \begin{align} \Phi_{Z_n}(s) &= E\left[e^{s\sum_{k=1}^n\frac{X_k}{\sqrt n}}\right] \\ &=E \left[\prod_{k=1}^ne^{s\frac{X_k}{\sqrt n}}\right] \\ &=\prod_{k=1}^nE\left[e^{s\frac{X_k}{\sqrt n}}\right] \\ &=\prod_{k=1}^n\Phi_X\left(\frac{s}{\sqrt n}\right) \\ &=\left(\Phi_X\left(\frac{s}{\sqrt n}\right)\right)^n \end{align} $

Let L(s) = log$ |phi_X $(s). Then, to show that

$ \Phi_{Z_n}(s)\rightarrow e^{\frac{s^2}{2}} $

it is sufficient to show that

$ nL\left(\frac{s}{\sqrt n}\right)=\log\left[\left(\Phi_X\left(\frac{s}{\sqrt n}\right)\right)^n\right]\rightarrow\frac{s^2}{2} $

Will need

$ \begin{align} & L(0)=0 \\ & L'(0)=\mu=0 \\ & L''(0)=E\left[X^2\right]=1 \\ \end{align} $

Now

$ \begin{align} \lim_{n\rightarrow\infty} nL\left(\frac{s}{\sqrt n}\right)&=\lim_{n\rightarrow\infty}\frac{L\left(\frac{s}{\sqrt n}\right)}{n^{-1}} \\ &= \lim_{n\rightarrow\infty} \frac{-L'\left(\frac{s}{\sqrt n}\right)n^{-\frac{3}{2}}s}{-2n^{-2}} \quad (\mbox{L}'\mbox{Hopital}) \\ &=\lim_{n\rightarrow\infty} \frac{L'\left(\frac{s}{\sqrt n}\right)s}{2n^{-\frac{1}{2}}} \\ &= \lim_{n\rightarrow\infty} \frac{-L''\left(\frac{s}{\sqrt n}\right)n^{-\frac{3}{2}}s^2}{-2n^{-\frac{3}{2}}} \quad (\mbox{L}'\mbox{Hopital again}) \\ &=\lim_{n\rightarrow\infty} \frac{L''\left(\frac{s}{\sqrt n}\right)s^2}{2} \\ &=\frac{s^2}{2} \end{align} $

For general $ \mu $, $ \sigma^2 $, use the result for $ \mu $ = 0, $ \sigma^2 $ = 1 with

$ Y_k = \frac{X_k-\mu}{\sigma} $


References


Questions and comments

If you have any questions, comments, etc. please post them on this page


Back to all ECE 600 notes

Retrieved from "https://www.projectrhea.org/rhea/index.php?title=ECE600_F13_Stochastic_Convergence_mhossain&oldid=66220"
Shortcuts
Help Main Wiki Page Random Page Special Pages Log in
Search

Alumni Liaison

Correspondence Chess Grandmaster and Purdue Alumni

Prof. Dan Fleetwood