ECE600 F13 Joint Expectation mhossain - Rhea

Back to all ECE 600 notes

Joint Expectation

Given random variables X and Y, let Z = g(X,Y) for some g:R$ _2 $→R. Then E[Z] can be computed using f$ _Z $(z) or p$ _Z $(z) in the original definition of E[ ]. Or, we can use

The proof is in Papoulis.

We will use joint expectation to define some important moments that help characterize the joint behavior of X and Y.

Note that joint expectation is a linear operator, so if g$ _1 $,...,g$ _n $ are n functions from R$ ^2 $ to R and a$ _1 $,...,a$ _n $ are constants, then

Important Moments for X,Y

We still need $ \mu_X $, $ \mu_Y $, $ \sigma_X $$ ^2 $, $ \sigma_X $$ ^2 $, the means and variances of X and Y. Other moments that are of great interest are:

• The correlation between X and Y is
  

• The covariance of X and Y
  

• The correlation coefficient of X and Y is
  

• Note:
  • |r$ _{XY} $| ≤ 1 (proof)
  • If X and Y are independent, then r$ _{XY} $ = 0. The converse is not true in general.
• If r$ _{XY} $=0, then X and Y are said to be uncorrelated. It can be shown that
  • X and Yare uncorrelated iff Cov(X,Y)=0 (proof).
  • X and Y are uncorrelated iff E[XY] = $ \mu_X\mu_Y $ (proof).
• X and Y are orthogonal if E[XY]=0.

The Cauchy Schwarz Inequality

For random variables X and Y,

with equality iff Y = a$ _0 $X with probability 1, where a$ _0 $ is a constant. Note that "equality with probability 1" will be defined later.

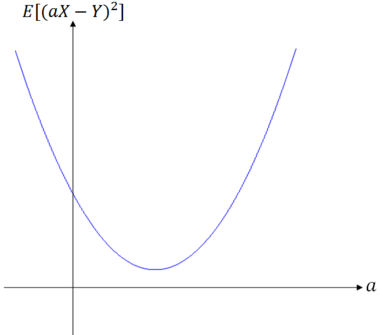
Proof: $ \qquad $ We start by considering

which is a quadratic function of a ∈ R. Consider two cases:

(i)$ \; $ E[(aX-Y)^2] > 0

(ii) E[(aX-Y)^2] = 0

Case (i):

Fig 1: A possible depiction of the quadratic when the discriminant is greater than zero.

Since this quadratic is greater than 0 for all a, there are no real roots. There must be two complex roots. From the quadratic equation, this means that

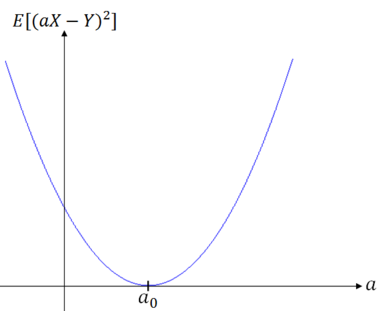
Case (ii):

In this case

Fig 2: A possible depiction of the quadratic when the discriminant is equal to zero.

This means that ∃a ∈ R such that

It can be shown that if a random variable X has E[X$ ^2 $]=0, then X=0 except possibly on a set of probability 0. Note that previously, we have defined equality between random variables X and Y to mean

With the same notion of equality, we would have that

However, the result for the case E[X$ ^2 $]=0 is that X=0 with probability 1, which means that there is a set A = {$ \omega $ ∈ S: X($ \omega $) = 0} with P(A) = 1.

Returning to the case E[(a$ _0 $X-Y)$ ^2 $]=0, we get that Y = a$ _0 $X for some a$ _0 $ ∈ R, with probability 1.
Thus we have shown that

with equality iff Y = a$ _0 $X with probability 1.

The Correlation Coefficient for Jointly Gaussian Random Variables X and Y

We have previously seen that the joint density function for Gaussian X and Y contains a parameter r. It can be shown that this r is the correlation coeffecient of X and Y:

Note that one way to show this is to use a concept called iterated expectation, which we will cover later.

Joint Moments

Definition $ \qquad $ The joint moments of X and Y are

and the joint central moments are

for j = 0,1,...; k = 0,1,...

Joint Characteristic Function

Definition $ \qquad $ The joint characteristic function of X and Y is

for $ \omega_1,\omega_2 $ ∈ R.

If X and Y are continuous, we write this as

If X and Y are discrete, we use

Note:

$ \bullet\; \Phi_X(\omega)=\Phi_{XY}(\omega,0);\quad\Phi_Y(\omega)=\Phi_{XY}(0,\omega) $

(proof)

$ \bullet\; Z = aX+bY \;\Rightarrow\;\Phi_Z(\omega) =\Phi_{XY}(a\omega,b\omega) $

(proof)

$ \bullet\; X \perp\!\!\!\perp Y \;\mbox{iff}\;\Phi_{XY}(\omega_1,\omega_2)=\Phi_X(\omega_1)\Phi_Y(\omega_2) $

(proof)

$ \bullet\; X \perp\!\!\!\perp Y \;\mbox{and}\;Z=X+Y\;\Rightarrow\Phi_{Z}(\omega)=\Phi_X(\omega)\Phi_Y(\omega) $

(proof)

Moment Generating Function

The joint moment generating function of X and Y is

Then it can be shown that

References

• M. Comer. ECE 600. Class Lecture. Random Variables and Signals. Faculty of Electrical Engineering, Purdue University. Fall 2013.

Questions and comments

If you have any questions, comments, etc. please post them on this page

Back to all ECE 600 notes