ECE600 F13 Joint Distributions mhossain - Rhea

Back to all ECE 600 notes

Two Random Variables

We have been considering a single random variable X and introduces the pdf f$ _X $, and pmf p$ _X $, conditional pdf f$ _X $(x|M), the conditional pmf p$ _X $(x|M), pdf f$ _Y $ or pmf p$ _Y $ when Y = g(X), expectation E[g(X)], conditional expectation E[g(X)|M], and characteristic function $ \Phi_X $. We will now define similar tools for the case of two random variables X and Y.
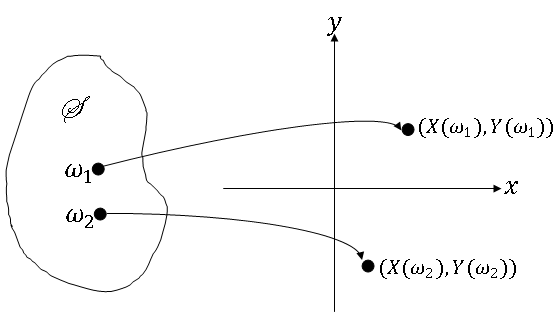
How do we define two random variables X,Y on a probability space (S,F,P)?

Fig 1: Mapping from S to X($ \omega $) and Y($ \omega $).

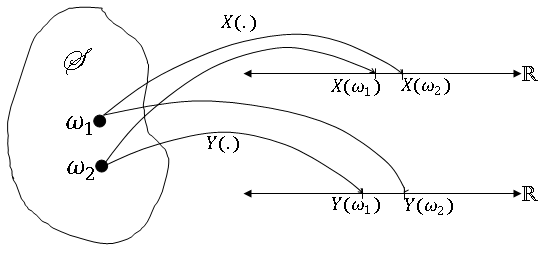
So two random variables can be viewed aw a mapping from S to R$ ^2 $, and (X,Y) is an ordered pair in R$ ^2 $. Note that we could draw the picture this way:

Fig 2: Mapping from S to X($ \omega $) and Y($ \omega $). Note that this model does not capture the joint behavior of X and Y and is hence incomplete.

but this would not capture the joint behavior of X and Y. Note also that if X and Y are defined on two different probability spaces, those two spaces can be combined to create (S,F,P).

In order for X and Y to be a valid random variable pair, we will need to consider regions D ⊂ R$ ^2 $.

We need {(X,Y) ∈ O} ∈ F for any open rectangle O ⊂ R$ ^2 $, then {(X,Y) ∈ D} ∈ F ∀D ∈ B(R$ ^2 $).
But (X($ \omega $),Y($ \omega $)) ∈ O if X($ \omega $) ∈ A and Y($ \omega $) ∈ B for some A, B ∈ B(R), so {(X,Y) ∈ O} = X$ ^{-1} $(A) ∩ Y$ ^{-1} $(B)
If X and Y are valid random variables then

So,

So how do we find P((X,Y) ∈ D) for D ∈ B(R$ ^2 $)?

We will use joint cdfs, pdfs, and pmfs.

Joint Cumulative Distribution Function

Knowledge of F$ _X $(x) and F$ _Y $(y) alone will not be sufficient to compute P((X,Y) ∈ D) ∀D ∈ B(R$ ^2 $), in general.

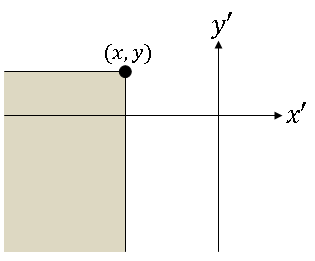
Definition $ \qquad $ The joint cumulative distribution function of random variables X,Y defined on (S,F,P) is F$ _{XY} $(x,y) ≡ P({X ≤ x} ∩ {Y ≤ y}) for x,y ∈ R.
Note that in this case, D ≡ D$ _{XY} $ = {(x',y') ∈ R$ ^2 $: x' ≤ x, y' ≤ y}

Fig 3: The shaded region represents D

Properties of F$ _{XY} $:

$ \bullet\lim_{x\rightarrow -\infty}F_{XY}(x,y) = \lim_{y\rightarrow -\infty}F_{XY}(x,y) = 0 $
$ \begin{align} \bullet &\lim_{x\rightarrow \infty}F_{XY}(x,y) = F_Y(y)\qquad \forall y\in\mathbb R \\ &\lim_{y\rightarrow \infty}F_{XY}(x,y) = F_X(x)\qquad \forall x\in\mathbb R \end{align} $
F$ _X $ and F$ _Y $ are called the marginal cdfs of X and Y.
$ \bullet P(\{x_1 < X\leq x_2\}\cap\{y_1<Y\leq y_2\}) = F_{XY}(x_2,y_2)-F_{XY}(x_1,y_2)-F_{XY}(x_2,y_1)+F_{XY}(x_1,y_1) $

The Joint Probability Density Function

Definition $ \qquad $ The joint probability density function of random variables X and Y is

∀(x,y) ∈ R$ ^2 $ where the derivative exists.

It can be shown that if D ∈ B(R$ ^2 $), then,

where D ≡ D$ _{XY} $ = {(x',y') ∈ R$ ^2 $: x' ≤ x, y' ≤ y}

Properties of f$ _{XY} $:

$ \bullet f_{XY}(x,y)\geq 0\qquad\forall x,y\in\mathbb R $
$ \bullet \int\int_{\mathbb R}f_{XY}(x,y)dxdy = 1 $
$ \bullet F_{XY}(x,y) = \int_{-\infty}^{y}\int_{-\infty}^xf_{XY}(x',y')dx'dy'\qquad\forall(x,y)\in\mathbb R^2 $
$ \begin{align} \bullet &f_X(x) = \int_{-\infty}^{\infty}f_{XY}(x,y)dy \\ &f_Y(y) = \int_{-\infty}^{\infty}f_{XY}(x,y)dx \end{align} $ are the marginal pdfs of X and Y.

The Joint Probability Mass Function

If X and Y are discrete random variables, we will use the joint pdf given by

Note that if X is continuous and Y discrete (or vice versa), we will be interested in

We often use a form of Bayes' Theorem, which we will discuss later, to get this probability.

Joint Gaussian Random Variables

An important case of two random variables is: X and Y are jointly Gaussian if their joint pdf is given by

where μ$ _X $, μ$ _Y $, σ$ _X $, σ$ _Y $, r ∈ R; σ$ _X $,σ$ _Y $ > 0; -1 <r <1.

It can be shown that is X and Y are jointly Gaussian then X is N(μ$ _X $, σ$ _X $$ ^2 $) and Y is N(μ$ _Y $, σ$ _Y $$ ^2 $) (proof)

Special Case

We often model X and Y as jointly Gaussian with μ$ _X $ = μ$ _Y $ = 0, σ$ _X $ = σ$ _Y $ = σ, r = 0, so that

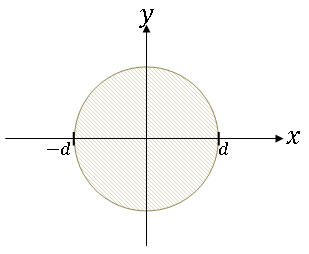
Example $ \qquad $ Let X and Y be jointly Gaussian with μ$ _X $ = μ$ _Y $ = 0, σ$ _X $ = σ$ _Y $ = σ, r = 0. Find the probability that (X,Y) lies within a distance d from the origin.

Let

Fig 4:The shaded region shows D$ _d $ = {(x,y)∈R$ ^2 $: x$ ^2 $+y$ ^2 $ ≤ d}

Then

Use polar coordinates to make integration easier: let

Then

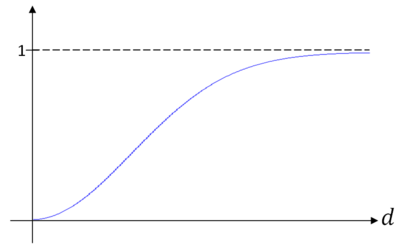
So the probability that (X,Y) lies within distance d from the origin looks like the graph in figure 5 (as a function of d).

Fig 5: P({X$ ^2 $,Y$ ^2 $ ≤ d}) plotted as a function of d

References

• M. Comer. ECE 600. Class Lecture. Random Variables and Signals. Faculty of Electrical Engineering, Purdue University. Fall 2013.

Questions and comments

If you have any questions, comments, etc. please post them on this page

Back to all ECE 600 notes