ECE600 F13 Conditional probability mhossain - Rhea

Topic 3: Conditional Probability and Total Probability Law

Conditonal Probability

For any event A ∈ F, we have P(A) representing the probability of A occurring. What if we want to know the probability of A given that we know another event, B, has occurred?

e.g. Roll a fair die ⇒ S = {1,2,3,4,5,6}
Consider A = {2,4,6} i.e. the event that the outcome is even
Then P(A) = $$ 1/2 $$ since the die is fair.
Let B = {4,5,6} i.e. the event that you roll a number greater than 3.
Then, what is the probability of A conditional on B occurring? It is not the same as P(A).
Intuitively, we know that if B occurs, then A occurs if the outcome is either 4 or 6. Since 4 and 6 represent two of the three equally likely outcomes in B, it makes sense that the probability of A given B is $$ 2/3 $$ .

We need a more general and rigorous mathematical approach to conditional probability.

Definition $\qquad$ Given A,B ∈ F, the conditional probability of A given B is

P(A|B) \equiv \frac{P(A\cap B)}{P(B)}, \;\; P(B)\ge 0

If P(B) = 0, then P(A|B) is undefined.

For our example above, P(A ∩ B) = p({4,6}) = 1/3
so, P(A|B) = 2/3

Note that it can be shown using the axioms that

P(\cdot|B):\mathcal F \rightarrow\mathbb R

is a valid probability measure for any B in the event space such that P(B)>0. Then (S,F,P(.|B)) is a valid probability space (proof).

Some properties of P(A|B):

if A ⊂ B, then P(A|B) = P(A)/P(B) ≥ P(A)
if B ⊂ A, then P(A|B) = P(B)/P(B) = 1
if A ∩ B = ø, then P(A|B) = P(ø|B) = 0

Bayes' Theorem

Let (S,F,P(.|B)) be a probability space and let A,B be elements of the event space F. We can write

\begin{align} P(A|B) &= \frac{P(A\cap B)}{P(B)}\; \mbox{and} \\ P(B|A) &= \frac{P(A\cap B)}{P(A)} \end{align}

so that

\begin{align} P(A|B)P(B) &= P(B|A)P(A) \\ \Rightarrow P(A|B) &= \frac{P(B|A)P(A)}{P(B)} \end{align}

assuming both P(A) and P(B) are greater than zero. This expression is referred to as Bayes' Theorem. We will see other equivalent expressions when we cover random variables.

This formula is very useful when we need P(A|B) and we know only P(B|A), P(A) and P(B).

For more on Bayes' Theorem you might want to check out this Math Squad tutorial.

Total Probability

Let $$ A_1,...,A_n $$ be a partition of S, and let B be an event in the event space F. Then the total probability law states that

P(B) =\sum_{i=1}^n P(B|A_i)P(A_i)

Proof:

\begin{align} P(B) &= P(B\cap\mathcal S) \\ &= P\left(B\cap\left(\bigcup_{i=1}^n A_i\right)\right) \\ &= P\left(\bigcup_{i=1}^n\left(B\cap A_i\right)\right) \\ &= \sum_{i=1}^n P(B\cap A_i)\\ &=\sum_{i=1}^n P(B|A_i)P(A_i) \end{align}

An example Problem

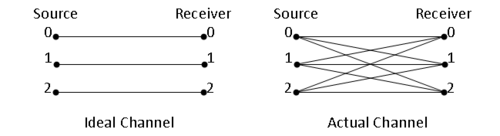
Consider a communication channel with a three symbol alphabet shown in figure 1.

Fig 1

\mathcal S = \{(i,j):\;i\;\mbox{is sent, } j\; \mbox{is receieved}, \;i,j=0,1,2\}

Consider the event $\{(i,0),(i,1),(i,2)\}$ for some $$ i $$ =0,1 or 2
This is the event that the symbol $$ i $$ was sent
Likewise, $\{(0,j),(1,j),(2,j)\}$ for some $$ j $$ =0,1 or 2, is the event that the symbol $$ j $$ was received
If we let $$ i = 0 $$ , then $A = \{(0,0),(0,1),(0,2)\}$ .
If $$ j = 0 $$ , then $B = \{(0,0),(1,0),(2,0)\}$ .
We want to know the probability that a 0 was sent and a 0 was received, i.e., we want to know

P(A|B)=P(0 \;\mbox{sent}|0\;\mbox{received})

Using Bayes' Theorem, we have that

P(0\;\mbox{sent}|0\;\mbox{received}) = \frac{P(0\;\mbox{received}|0\;\mbox{sent})\;P(0\;\mbox{sent})}{P(0\;\mbox{received})}

Now we need:

P(0 received|0 sent). In practice, we use channel modelling to estimate this for every i and j.
We also need P(0 sent). Use source modelling to approximate this.
Finally, we need P(0 received). We will typically get this using total probability.

P(0\;\mbox{sent}) = \sum_{i=0}^2 P(0\;\mbox{received}|i\;\mbox{sent})P(i\;\mbox{sent})

Then

P(0\;\mbox{sent}|0\;\mbox{received}) = \frac{P(0\;\mbox{received}|0\;\mbox{sent})P(0\;\mbox{sent})}{\sum_{i=0}^2 P(0\;\mbox{received}|i\;\mbox{sent})P(i\;\mbox{sent})}

References

M. Comer. ECE 600. Class Lecture. Random Variables and Signals. Faculty of Electrical Engineering, Purdue University. Fall 2013.

Questions and comments

If you have any questions, comments, etc. please post them on this page

Back to all ECE 600 notes
Previous Topic: Probability Spaces
Next Topic: Statistical Independence