ECE600 F13 Conditional Expectations for Two Random Variables mhossain - Rhea

Topic 16: Conditional Expectation for Two Random Variables

If X and Y are random variables on (S,F,P) and ∈ F with P(M) > 0, then,

E[g(X,Y)|M] = \int\int_{\mathbb R^2} g(x,y)f_{XY}(x,y|M)dxdy

One important case is when M = {Y = y} for some y ∈ R. Then we have that

E[g(X,Y)|Y=y]=\int\int_{\mathbb R^2}g(x,y')f_{XY}(x,y'|Y=y)dxdy'

Using our old trick, let

E[g(X,Y)|Y=y]=\lim_{\Delta y\rightarrow 0}\int\int_{\mathbb R^2}g(x,y')f_{XY}(x,y'|y<Y\leq y+\Delta y)dxdy'

Using this approach, it can be shown that

\begin{align} E[g(X,Y)|Y=y]&=E[g(X,y)|Y=y] \\ &=\int_{-\infty}^{\infty}g(x,y)f_{X|Y}(x|y)dx \\ \end{align}

Another important case: g(X,Y)=g(X)

\begin{align} E[g(X)|M]&=\int\int g(x)f_{XY}(x,y|M)dxdy \\ &=\int g(x)\left[\int f_{XY}(x,y|M)dy\right]dx \\ &=\int g(x)f_X(x|M)dx \end{align}

Note that this is the same equation we had, for example

E[g(X)|Y=y]=\int g(x)f_{X|Y}(x|y)dx

Iterated Expectation

Sometimes we want to work with f $_{Y|X}$ (y|x) and f $$ _X $$ (x) instead of f $_{XY}$ (x,y). This can make computation of E[g(X,Y)] easier in some cases. We can write

\begin{align} E[g(X,Y)]&=\int\int_{\mathbb R^2}g(x,y)f_{XY}(x,y)dxdy \\ &=\int\int_{\mathbb R^2}f_X(x)g(x,y)f_{Y|X}(y|x)dydx \\ &=\int_{\mathbb R}f_X(x)E[g(X,Y)|X=x]dx \end{align}

Note that E[g(X,Y)|X=x] is a function of x ∈ R. We will call this function h.

h(x)=E[g(X,Y)|X=x]\qquad h:\mathbb R\rightarrow\mathbb R

We can create a random variable h(X). We will use the notation

E[g(X,Y)|X]\equiv h(X)

So we have

h(x) = E[g(X,Y)|X=x] \

which is a real-valued function of x ∈ R, and h(X), which is a random variable since it is a function of random variable X.

Now we can write

\begin{align} E[g(X,Y)]&=\int_{\mathbb R}E[g(X,Y)|X=x]f_X(x)dx \\ &= \int_{\mathbb R}h(x)f_X(x)dx \\ &=E[h(X)] \end{align}

So,

E[g(X,Y)] = E[E[g(X,Y)|X]] \

We call this iterated expectation.

An important special case is when g(X,Y)=Y, in which case, we have

E[Y]=E[E[Y|X]] \

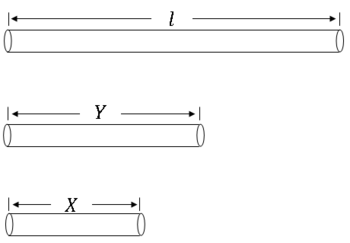
Example $\qquad$ Suppose we have a stick of length l. We break the stick at a uniformly chosen point Y, then again at a uniformly chosen point X. Find E[X].

Fig 1: example problem

\begin{align} E[X]&=\int\int_{\mathbb R^2}xf_{XY}(x,y)dxdy \\ &=\int_{\mathbb R}xf_X(x)dx \end{align}

We do not know f $_{XY}$ or f $$ _X $$ , but we know f $_{X|Y}$ or f $$ _Y $$

\begin{align} f_Y(y)&=\frac{1}{l}\qquad\ &0\leq y\leq l \\ f_{X|Y}(x|y)&=\frac{1}{y}\qquad &0\leq x\leq y \end{align}

Use E[X]=E[E[X|Y]]. Now

h(y)\equiv E[X|Y=y] = \frac{y}{2}

since X is uniform on [0,y] given Y=y. So,

h(Y)=\frac{Y}{2}

Then

E[X]=E\left[\frac{Y}{2}\right]=\frac{1}{2}E[Y]=\frac{1}{2}.\frac{l}{2}=\frac{l}{4}

References

M. Comer. ECE 600. Class Lecture. Random Variables and Signals. Faculty of Electrical Engineering, Purdue University. Fall 2013.

Questions and comments

If you have any questions, comments, etc. please post them on this page

Back to all ECE 600 notes

ECE600 F13 Conditional Expectations for Two Random Variables mhossain - Rhea

Iterated Expectation

References

Questions and comments

Alumni Liaison