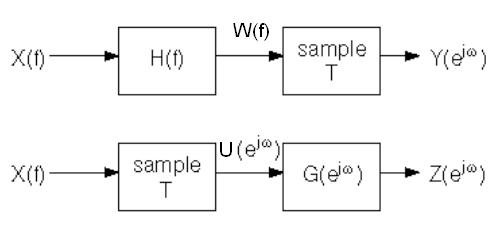
$ \begin{align} W(f) &= X(f) H(f) \\ Y(e^{j\omega}) &= \frac{1}{T} \sum_{l=-\infty}^{\infty} W \Bigg( \frac{\omega - 2l\pi}{2\pi T}\Bigg) \\ Y(e^{j\omega}) &= \frac{1}{T} \sum_{l=-\infty}^{\infty} X \Bigg( \frac{\omega - 2l\pi}{2\pi T}\Bigg)H \Bigg( \frac{\omega - 2l\pi}{2\pi T}\Bigg) \\ \\ U(e^{j\omega}) &= \frac{1}{T} \sum_{l=-\infty}^{\infty} X \Bigg( \frac{\omega - 2l\pi}{2\pi T}\Bigg) \\ Z(e^{j\omega}) &= U(e^{j\omega}) G(e^{j\omega}) \\ Z(e^{j\omega}) &= \frac{1}{T} \sum_{l=-\infty}^{\infty} X \Bigg( \frac{\omega - 2l\pi}{2\pi T}\Bigg) G(e^{j\omega}) \\ \end{align} $
$ \begin{align} G(e^{j\omega}) &= \sum_{k=-\infty}^{\infty} H \Bigg( \frac{\omega - 2k\pi}{2\pi T}\Bigg) \\ Z(e^{j\omega}) &= \Bigg(\frac{1}{T} \sum_{l=-\infty}^{\infty} X \Bigg( \frac{\omega - 2l\pi}{2\pi T}\Bigg)\Bigg)G(e^{j\omega}) \\ Z(e^{j\omega}) &= \frac{1}{T} \sum_{l=-\infty}^{\infty} X \Bigg( \frac{\omega - 2l\pi}{2\pi T}\Bigg)\sum_{k=-\infty}^{\infty} H \Bigg( \frac{\omega - 2k\pi}{2\pi T}\Bigg) \\ Z(e^{j\omega}) &= \frac{1}{T} \sum_{l=-\infty}^{\infty}\sum_{k=-\infty}^{\infty} X \Bigg( \frac{\omega - 2l\pi}{2\pi T}\Bigg) H \Bigg( \frac{\omega - 2k\pi}{2\pi T}\Bigg) \\ \end{align} $
Both X(f) and H(f) are bandlimited to 1/2T, so
$ \begin{align} Z(e^{j\omega}) &= \frac{1}{T} \sum_{l=-\infty}^{\infty} X \Bigg( \frac{\omega - 2l\pi}{2\pi T}\Bigg) H \Bigg( \frac{\omega - 2l\pi}{2\pi T}\Bigg) \\ Z(e^{j\omega}) &= Y(e^{j\omega}) \end{align} $
Credit: Prof. Charles Bouman
Back to ECE438_Week6_Quiz