Contents
[hide]ECE Ph.D. Qualifying Exam in Communication Networks Signal and Image processing (CS)
Question 5, August 2012, Part 1
- Part 1 , 2
Solution:
a) $ \gamma=1 $
b)
$ (x_r,y_r)=(\frac{a}{a+d+g},\frac{d}{a+d+g}) $
$ (x_g,y_g)=(\frac{b}{b+e+h},\frac{e}{b+e+h}) $
$ (x_b,y_b)=(\frac{c}{c+f+i},\frac{f}{c+f+i}) $
c)
$ (x_w,y_w)=(\frac{a+b+c}{a+b+c+d+e+f+g+h+i},\frac{d+e+f}{a+b+c+d+e+f+g+h+i}) $
d)
If $ (X,Y,Z)=(0,1/2,1/2) $, then $ (x,y)=(0,1/2) $.
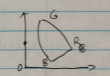
In the chromaticity diagram, this point is outside the horse shoe shape, so its RGB values are not all larger than 0 ($ R<0,G>0,B>0 $).
e) We are likely to see quantization artifact in dark region.
Related Problem
Consider a color imaging device that takes input values of $ (r,g,b) $ and produces ouput $ (X,Y,Z) $ values given by
$ \left[ {\begin{array}{*{20}{c}} X\\ Y\\ Z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} a&b&c\\ d&e&f\\ g&h&i \end{array}} \right]\left[ {\begin{array}{*{20}{c}} r^\alpha\\ g^\alpha\\ b^\alpha \end{array}} \right] $
a) Calculate the white point of the device in chromaticity coordinates.
b) What are the primaries associated with the r,g, and b components respectively?
c) What is the gamma of the device?
d) Draw the region on the chromaticity diagram corresponding to $ r < 0, g > 0, b > 0 $.