Bayes Rules under Severe Class Imbalance
Bayes decision rule is a simple, intuitive and powerful classifier. It allows to select the most likely class, given the information gathered. Here also lies an important limitation of this classifier, as relies heavily on the probability values associated to each class. In many real world scenarios, this might not be completely possible to collect.
An interesting experiment to test Bayes decision rule involves an scenario faced in my area of research, intrusion detection (in the context of computer systems). In this scenario, there exists a severe class imbalance between what is considered normal and malicious traffic (attacks). The prior probabilities of the classes can be several orders of magnitude different between them. Also, the problem worsens as the inter-class features can be highly correlated. Attackers try to hide behind normal traffic, therefore their malicious traffic correlates to the normal traffic.
Further information on this problem, known as the Bayes-Rate Fallacy, related to the intrusion detection field, is provided in [1]. Nevertheless, this problem is not exclusive to the computer security field, and a more general discussion on the class imbalance problem has been given by the statistical pattern recognition community, as shown in [2].
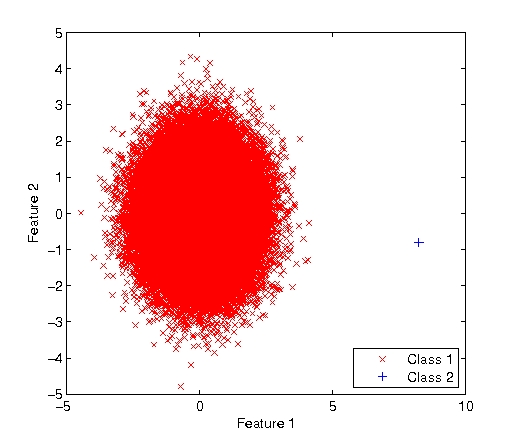
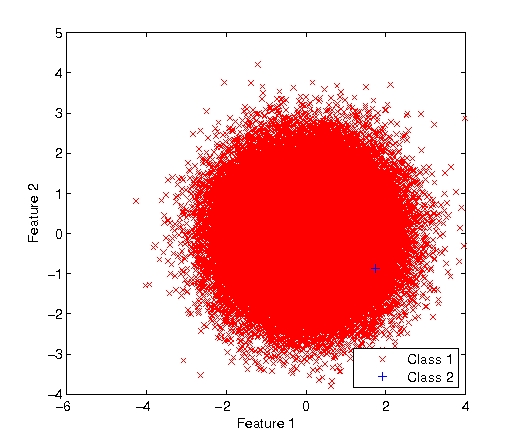
In this experiment, we decided to test the Bayes decision rule on two 2 − D classes with severe imbalance between them. Prior probabilities for both classes were defined as P(ω1) = 0.99999 and $ P(\omega_2) = 1 \times 10^{-5} $. Class ω1 has distribution with means μ1a = μ1b = 0, and covariance matrix $ \Sigma = 0.9 \times I_d $. We also start our experiment with identitical distribution for class ω2, then the mean of this class was changed and then the error rate computed. This was repeated for different values of the mean.
Looking at the results, the class imbalance makes it more difficult to accurately determine the correct class of a particular event or object. In Figure 1 (left, above), the mean of feature in class is μ2a = 8 so classes are highly uncorrelated. Problem with class imbalance is shown in Figure 2 (right, above), where μ2a = 3 and classifier incorrectly selects a class ω2 object as class ω1. As there are significantly fewer occurances of class ω2 than ω1 in the universe under consideration, mistakes are most costly. Also, to correctly classify each of these occurances, one might be tempted to increase the sensitivity of the classifier which would (unfortunately) also increase the number of false positive cases. At the end, this problem is not caused by the Bayesian decision rule. But one as a researcher should be aware that additional techniques should be considered to effectively classify objects under the class imbalance scenario.
--Gmodeloh 14:55, 13 April 2010 (UTC)
References
[1] S. Axelsson: The base-rate fallacy and the difficulty of intrusion detection. In: ACM Trans. Inf. Syst. Secur., pp. 186–205. ACM, New York, 2000.
[2] C. Drummond and R. Holte: Severe Class Imbalance: Why Better Algorithms Aren’t the Answer. In: J. Gama et al. (Eds.): ECML 2005, LNAI 3720, pp. 539–546. Springer-Verlag, Berlin Heidelberg, 2005.
Depends on how you define this problem. If the misclassification is equal-costly, then in this problem, you just always classify it as one, and you achieve almost 100% success rate! Hooray! But, it makes the problem very uninteresting. So I guess the correct words to define the problem is to detect abnomaly (class2) from samples (class1). In the first example, it's probably do-able, since the abnomal sample is made far apart enough (compared to the variance of class1), but in the second example, it's just not possible to ditinguish. More features need to be added.
--Ding6