Problem 2
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
By considering the terms in the Fibonacci sequence whose values do not exceed four million, find the sum of the even-valued terms.
Fibonacci sequence is often used to illustrate the efficacy of dynamic programming (link to MIT Lecture on Dynamic Programming). But, as it turns out, I was the naive one in thinking that dynamic programming will be the Little Gauss approach to solve this problem.
The Naive
The solution can be very simple:
1. Declare two variable x := 1 and y:= 2 2. Declare variable sum := 2 3. While x + y is less than 4,000,000 -3.a Let x := x + y (on alternate iterations let y := x + y) -3.b If x/y is divisible by 2, add to the sum
An example of implementation of the above algorithm is here
Little Gauss
The reason I had believed that dynamic programming would be more efficient is that it is, indeed, much more efficient in generating Fibonacci sequence than the recursive method (recursive example). But I am no longer sure whether generation of Fibonacci sequence is in dynamic fashion is any more effective then the naive approach. Time-wise, it appears that the dynamic approach is actually slower than the naive approach.
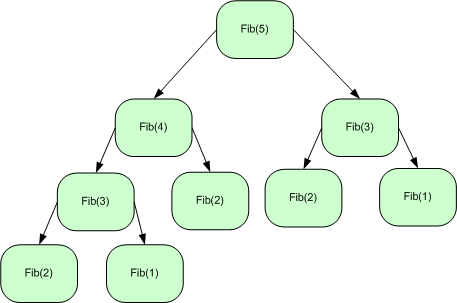
Regardless, maybe I should dedicate some time in explanation of dynamic programming instead of the solution. For this particular case, notice that if we were to use the recursive method for generating Fibonacci numbers, we are faced with repetitive sub-problems. For instance, if we want to know the 5th Fibonacci number:
Note that in calculating Fibonacci numbers:
Fib(1) was called 2 times Fib(2) was called 3 times Fib(3) was called 2 times Fib(4) was called 1 time Fib(5) was called 1 time
Therefore, we had to calculate nth Fibonacci number more than once. Because each call of Fib begets two additional sub-problems, recursive method for generating fibonacci number has complexity of $ O(2^{n}) $
However, suppose we create an internal system within the program that takes note of what the nth Fibonacci number is. Then, whenever Fib(n) is called, the program will first check its notes for whether or not it had already calculated Fib(n) before, and if it did, it would simply recall that value. If it did not, it will look up Fib(n-1) and Fib(n-2), see if those values had been calculated before, and upon calculation will make a new note for F(n). This process is called memoization, and it greatly reduces the complexity of Fibonacci sequence program.
Then, what is so dynamic about dynamic programming?
"The dynamic programming paradigm was developed by Richard Bellman in the mid-1950s, while working at the RAND Corporation. Bellman deliberately chose the name ‘dynamic programming’ to hide the mathematical character of his work from his military bosses, who were actively hostile toward anything resembling mathematical research. Here, the word ‘programming’ does not refer to writing code, but rather to the older sense of planning or scheduling, typically by filling in a table." -Jeff Ericson, http://www.cs.uiuc.edu/~jeffe/teaching/algorithms/notes/