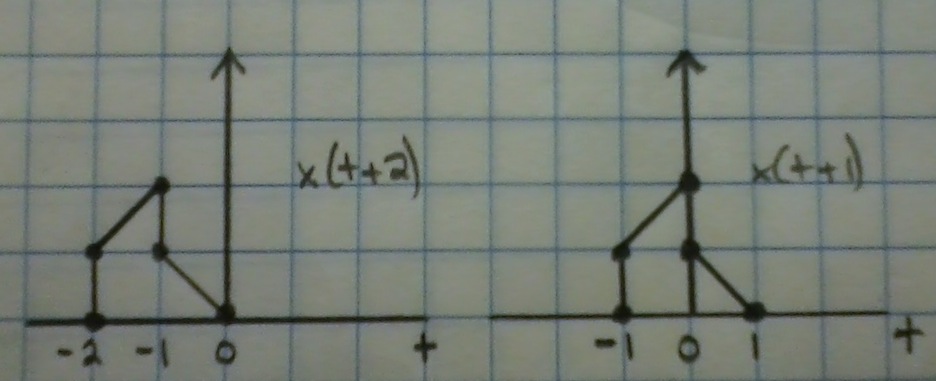Contents
[hide]Linearity
Linear system: y[n] = 8x[n/4]
Non-linear system: y(t) = 5x^2(t) + 11
Causality
Causal system: y[n] = x[n] + x[n-4]
Non-causal system: y(t) = 3x(-t/6)
Memory
System w/ memory: y[n] = 3t^2x[n-9]
Memoryless system: y(t) = (4x(t))^2
Invertibility
Invertible system: y[n] = 2x[n+4]
Non-invertible system: y(t) = x^4(t) -5
Stability
Stable system: y[n] = x^2[n] +4x[n] -1
Non-stable system: y(t) = d^2x(t)/dt^2 + dx(t)/dt + 6x(t)
Time Invariance
Time-variant system: y[n] = 3n^2x[n] + 5
Time-invariant system: y(t) = 2x(t) + x(t-3)
Question
Determine and sketch the convolution of the following signals:
x(t) = t+1 for $ 0 \le t \le 1 $
x(t) = 2-t for $ 1 < t \le 2 $
x(t) = 0 everywhere else
h(t) = $ \delta(t+2) $ + $ 2\delta(t+1) $
Solution
x(t)*h(t) = $ \int x(\tau)h(t-\tau)d\tau $ = $ \int h(\tau)x(t-\tau)d\tau $
Becomes x(t)*h(t) = x(t+2)+2x(t+1)
Sketches:
y(t) = t+3 for $ -2 < t \le -1 $
y(t) = t+4 for $ -1 < t \le -0 $
y(t) = 2-2t for $ 0 < t \le 1 $
y(t) = 0 everywhere else
Question
Determine the fundamental period of the signal x(t) = 5cos(14t)+sin(6t-2).
Solution
Period of first term = $ \frac{2\pi}{14} $ = $ \frac{\pi}{7} $
Period of second term = $ \frac{2\pi}{6} $ = $ \frac{\pi}{3} $
Least common multiple = Fundamental period = $ \pi $
Please place solutions and/or comments below.