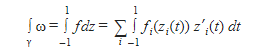Integration and Derivation on Riemann Surfaces
It is no easy task to integrate on a Riemann Surface. First, each path (γ) of the surface must be broken up into a finite number of paths {γi}such that all γi are always differentiable for all degrees. Then, ω can express a differentiable portion of the surface, representing fi(zi)dzi, where z is parameterized as zi(t) and t ∈ [-1,1] using each γi path. Finally, the integral can be written as:
Put simply, the surface is interpreted as its atlas, or the set of charts, aka graphs that roughly describe the surface at a certain point, and the integral of the surface is solved by taking the sum of the integrals of all of the charts from -1 to 1. The third version of the integral equation is similar to how the parametric vector form for line integrals of vector fields is set up. This integral can be used to find the amount of space under the Riemann Surface, just like any “regular” integral.
Derivatives are taken of the map between two Riemann Surfaces, X and Y at a specific point. This derivative is not a number, but a linear map in a complex space. This is done using OX,x, a group of differentiable functions roughly equivalent to X about a neighborhood around x and also near Y. Next, we define a tangent space, a plane of possible movement vectors, of the Riemann Surface as TX,x</sub> , where X represents the Riemann Surface and x is the point where the derivative is being taken on the surface. Additionally, τX,x is the mapping of OX,x to the Complex plane. Finally, the derivative at x, Dx is the function that maps TX,x to TY,y.
It is difficult to express exactly what the derivative is. Like all derivatives, it represents how a function is changing at a specific point. For Riemann Surfaces, derivatives are found to understand how the mapping function between two surfaces changes and also represents the function mapping the tangent spaces of the surfaces.