Hilbert’s Nullstellensatz: Proofs and Applications
Author: Ryan Walter
Table of Contents:
1. Introduction
2. Vocab
3. Theorem
- Basis Theorem
- Weak Nullstellensatz
- Strong Nullstellensatz
4. Applications
5. Sources and Further Reading
1. Introduction:
Hilbert's Nullstellensatz is a relationship between algebra and geometry that was discovered by David Hilbert in 1900. Nullstellensatz is a German word that translates roughly to “Theorem of Zeros” or more precisely, “Zero Locus Theorem.” The Nullstellensatz is a foundational theorem that greatly advanced the study of algebraic geometry by proving a strong connection between geometry and a branch of algebra called commutative algebra. The Nullstellensatz also serves to connect algebraic geometry and abstract algebra. Both the Nullstellensatz and commutative algebra focus heavily on ‘rings,’ which will be defined in the vocabulary section. For example, it would be easier to use algebra than geometry to know more about a Togliatti surface, which is the shape below.
2. Vocab:
Polynomial Ring: A polynomial ring is defined as R[x] = R0x0 + R1x1+…+Rnxn, where R0, R1, … Rn are all coefficients in R. This polynomial ring is not a function and these x’s are not replaced by numbers; they are a symbol rather than a value. . Usually, when and R term is zero, the entire term is omitted.
Example: R(x) = 1 + 2x + 0x2 + 0x3 + 0x4 + 3x5 can be written as R(x) = 1 + 2x + 3x5
Ideals: An two-sided ideal, or simply ideal, of a ring is a special type of ring where any two numbers that are part of the set R, are also part of the set I when added together (a,b ∈ I, a+b ∈ I) and when a number from ring I and a number from the ring R are multiplied together, the product are a part of ring I. (a ∈ I, r ∈ R, ar ∈ I). In this definition, R is any given ring and I is a subset of R.
The ideal can be split further into left and right ideals, where a left ideal is found when sL∈ L, and a right ideal is found when Rs ∈ R. The order of multiplication is significant because the ideals are often displayed as matrices, and the order of multiplication is significant when multiplying matrices. In order for a ideal to be two-sided, it must be both a right and left ideal. In this definition, R is a set that is right-handed, L is a set that is left-handed, and s is a subset of L and R.
Examples:
{0} is an ideal for every ring, and is known as the trivial ideal.
The matrix below is the left ideal for every 2x2 matrix with real numbers.
0 1 0 1
Proof: Given the matrix of the set of R, we check by verifying sL∈ L
s L sL 0 1 * a b = 0a+1c 0c+1d = c d 0 1 c d 0a+1c 0c+1d c d
sL only has two elements, c and d, which are elements of L. Therefore, this s is a left ideal for all 2x2 matrices.
The matrix below is the right ideal of a ring for all 2x2 matrix with real numbers.
1 1 0 0
Proof: Given the matrix of the set of R, we check by verifying Lr ∈ L
R s Rs a b * 1 1 = 1a+0b 1a+0b = a a c d 0 0 1c+0d 1c+0d c c
Rs only has two elements, a and c, which are elements of R. Therefore, this s is a right ideal for all 2x2 matrices.
Algebraically closed: A field is algebraically closed if every polynomial ring’s coefficient f∈A has a root that is also in A. More simply, this means that there exists some x∈A where f(x) = 0. It is important to note that no finite field can be algebraically closed, because if the points are f1 , f2, .. fn, then the polynomial (x-f1)(x-f2)…(x-fn)+1 has no zeros that are a part of F.
Examples: x2+1 =0. A field comprised of only real numbers is not algebraically closed because there are no real numbers that can solve this polynomial despite the fact that the polynomial has real coefficients (0s and 1s).
Maximal Ideal: A maximal ideal is the ideal I of a ring R where I and R are the closest that they can be. Alternatively, if M is an ideal with I as a subset of M, then M must be either I or R.
Example: kR is a maximal ideal of R if k is prime and R is a ring of integers.
Vanishing Set: In this definition, V ⊆ R and (I(V)) ⊆ R. Additionally, V is a set with variety V. A vanishing set, which is noted as (I(V)), is a set of polynomials that ‘vanish’ on all points in V. Vanishing means that the terms all become zero, and is still present but often omitted for reduce clutter. (I(V)) is also an ideal, since when (I(V)) is multiplied with the ring, all terms of the subset V go to zero and the remaining terms are a part of R.
Noetherian Ring: A Noetherian Ring is another special type of ring where every ideal of the ring is a subset of the ring itself. All the ideals of the ring must also be finitely generated, which means that there is only a finite amount of combinations of sets.
Similar to the ideal, Noetherian Rings can be split into left and right Noetherian Rings. A ring is right Noetherian if it does not contain infinite sets of progressively larger right ideals, and likewise for the left Noetherian Ring. This is known as fulfilling the ascending chain condition for left or right ideals.
Radical Ideal: The radical ideal, denoted by √I, is an ideal in which fn and f are both elements of I when n is greater than or equal to one. (fn ∈ I and f ∈ I, n ≥ 1).
3. Theorem:
The Nullstellensatz comes in two forms, the weak and strong forms. However, they actually prove the same thing, and the weak Nullstellensatz is just a more focused version of the strong Nullstellensatz. After proving the weak Nullstellensatz, I will use the "Trick of Rabinowitsch" which uses the weak Nullstellensatz to prove the strong one.
a. Basis Theorem:
If a ring R is Noetherian, then R(x1,x2,...,xn) is also Noetherian, and in opposite fashion, if F(x1,x2,..,xn) is Noetherian, any field F is Noetherian. (Williams)
b. Weak Forms:
"Let K be an algebraically closed field, and let I ⊆ K[x1, x2, . . . , xn] be an ideal such that V(I) = ∅. Then I = K[x1, x2, . . . , xn]" (Williams)
Proof: First we will assume the first part of the weak Nullstellensatz, let K be an algebraically closed field, and let I ⊆ K[x1, x2, . . . , xn] be an ideal such that V(I) = ∅, when the symbol ∅ means an empty set. Because we know that V(I)) is an empty set, I(V(I)) is a set of polynomials that vanishes for an empty set. However, we know that any polynomial set would disappear when mixed with an empty set, so we can then say K[x1, x2, . . . , xn] = I(V(I)). From there, we use the identity that √I = I(V(I)), and write √I = K[x1, x2, . . . , xn]. Then, since K is any polynomial, we can say 1 ∈ √I, and using the definition of the radical ideal (fn ∈ I and f ∈ I, n ≥ 1) which implies that 1 ∈ I. Finally, we can write out the final product: I = K[x1, x2, . . . , xn], which is the weak Nullstellensatz.
c. Strong:
"Let I be an ideal of k[x1, . . . , xn], where k is algebraically closed. Suppose f ∈ k[x1, . . . , xn] vanishes on the vanishing set of I. Then there exists m ∈ N such that fr ∈ I." (Stanford)
Using “The Trick of Rabinowitsch” I will be adding another variable to the weak Nullstellensatz in order to prove the strong Nullstellensatz. First, I will assume the first part of the strong Nullstellensatz, let K be an algebraically closed field, and let I ⊆ K[x1, x2, . . . , xn]. Applying the Basis Theorem states that K and K[x1, x2, . . . , xn] are both Noetherian. For this proof, the ideal I will be written as (i1,i2,..ik) where all values of ik ∈ I. The introduction of another variable, y, gives a new ideal, I* ⊆ K[x1, x2, . . . , xn,y]. Relating the two ideals, I and I*, we can write I* with the terms from I. With this relation, I* can be written as (i1,i2,..ik, 1-yf). Using the weak Nullstellensatz here, there are no values in i that can make a zero in the 1-yf term. This generates the unit ideal for K[x1, x2, . . . , xn], which will be displayed as u1,u2,…,un. With this information, we can write the following equation:
1 = g0(x1, x2, . . . , xn)(1-x1 f( x2, . . . , xn) + $ \sum_{c=1}^{m} $ gi(x1, x2, . . . , xn) * fi(x1, x2, . . . , xn)
Substituting x1 = 1/f(x2,…,xn) gives the equation:
1 = $ \sum_{c=1}^{m} $ gi(1/f(x2, x3, . . . , xn), x2, x3, . . . , xn) * fi(x2, x3, . . . , xn)
Rewriting again to get a common denominator and returning g to a set from gives the equation:
1 = $ \sum_{i=0}^{n-1} i $ hi(x2, x3, . . . , xn) * fi(x2, x3, . . . , xn) / f(x2,...,xn)r
Multiplying both sides by the right’s denominator gives:
f(x2,...,xn)r = $ \sum_{c=1}^{m} $ hi(x2, x3, . . . , xn) * fi(x2, x3)
Which states the Nullstellensatz by showing that fr is a set of the ideal formed by the summation above.
Applications:
The Nullstellensatz has many applications in both geometry and algebraic geometry. One example of this is Buchberger's algorithm in geometry, which can be proven by starting with the Nullstellensatz. Combining Buchberger's algorithm with other geometric techniques helps prove difficult geometry applications and proofs. These two methods have been so successful in rationalizing difficult proof that they have been combined into software known as the Coq System. The Coq System is a program that can help you "execute algorithms and theorems together with an environment for semi-interactive development of machine-checked proofs" (Coq).
As mentioned in the introduction, Hilbert's Nullstellensatz was a foundational theorem for algebraic geometry, but it was actually what started the study of what we now call classical algebraic geometry. The Nullstellensatz works with the Fundamental Theorem of Algebra on multivariate polynomials in algebraically closed fields, which is a focus in classical algebraic geometry. Classical algebraic geometry also focuses on "classes of individual algebraic varieties, like points, curves and surfaces" (Konstanz). However, there are not many more discoveries happening in this field, because the studies in modern algebraic geometry are much more useful.
Another theorem that the Nullstellensatz can be used to prove is Stickelberger's theorem, which deals with annihilators in rings and ideals. An annihilator is similar to a vanishing set, where they both remove whatever sets they are combined with. Vanishing sets nullify sets, where annihilators nullify class groups. Just like the Nullstellensatz, Stickleberger looked heavily at ideals and sets and is primarily used to prove other theorems. Stickelberger's Theorem actually predates the Nullstellensatz by about ten years, but the Nullstellensatz simplifies the proof of Stickleberger's Theorem.
The Nullstellensatz can also be used to find whether polynomial problems have a solution or not when working on semidefinite programming problems. Semidefinite programming is studied not in computer science, but is applied in optimization and engineering. Semidefinite programming is a new, growing field which is most commonly used to optimize linear objective functions, meaning it will minimize or maximize the intersection of cones of matrices and an affine space. An affine space is a different kind of shape where some traditional Euclidian geometry but also loses some of its concepts, like distance or an origin.
Another use of the Nullstellensatz is proving the Ax-Grothendieck theorem, which discusses the relationship between a function's injective and bijective properties. It is valid for any function on an algebraically closed field. This theorem can be used to prove other theorems, such as the Garden of Eden theorem, and givens a more universal solution than other methods to prove the Garden of Eden Theorem. The Garden of Eden theorem says that in cellular automaton, there exist configurations that appear from nowhere, hence why they are named after the biblical story of the garden of Eden. It is apparent how far the Nullstellensatz reaches, because it can be used to prove theorems in fields that came to exist may years after the introduction of the Nullstellensatz. Cellular automaton is a very focused subject in computer science, which was discovered in the 1940's but was not studied extensively until the 1970s.
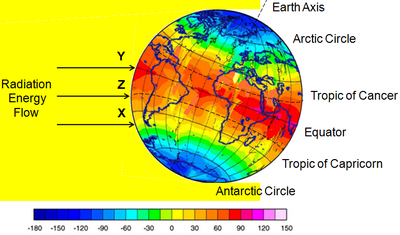
Furthermore, the Nullstellensatz can be used to prove theorems in other related fields, such as topography. The Borsuk-Ulam Theorum is an incredible theorem which can be proven using the Nullstellensatz, and the Borsak-Ulam Theroem, when applied, can prove there are always two points on opposite sides of Earth where there is equal temperature and pressure. The theorem says in a more universal way that any function on an n-sphere must have a pair of antipodal points.
Consider a simple example with only temperature:
The thought behind this is very similar to the mean value theorem from high school calculus. The temperature is not a constant at the equator, so choose any two points that are on opposite sides of the globe. However, to be certain this is true, we will assume that the temperature at each point is a continuous function, and doesn't change over time like the real Earth would. The two chosen points have different temperatures, and as you move around the globe, eventually the two points would have switched values after half a rotation. Since the values had the same magnitude of change, somewhere in between the two points, they were equal. However, the multivariate proof using the Nullstellensatz is much more difficult than this example.
Sources and Further Reading:
https://web.williams.edu/Mathematics/sjmiller/public_html/hudson/Sanderson-Nullstellensatz.pdf
https://stanford.edu/~sfh/nullstellensatz.pdf
https://artofproblemsolving.com/wiki/index.php/Polynomial_ring
https://mathworld.wolfram.com/NoetherianRing.html
http://www-groups.mcs.st-andrews.ac.uk/~john/MT4517/Lectures/L5.html
https://www.math.uchicago.edu/~may/PAPERS/MunshiFinal2.pdf
http://pi.math.cornell.edu/~dmehrle/notes/old/alggeo/23Nullstellensatz.pdf
https://arxiv.org/pdf/1809.02818.pdf
https://math.hmc.edu/funfacts/borsuk-ulam-theorem/
https://math.berkeley.edu/~bernd/cbms.pdf
Pictures: