Contents
Hyperbolic Spaces
Author: Zoe Egbert
Table of Contents
I. History/Development of Hyperbolic Spaces
II. Hyperboloid Model
III. Klein Model
IV. Poincare Disc Model
V. Art Based on Models
VI. Applications and Further Readings
Introduction
Hyperbolic space is an abstract concept of a place where hyperbolic geometry can exist. Hyperbolic spaces consist of negative curvatures that have properties significantly different from the most commonly known and understood, zero curvature of Euclidean space. The three main models commonly used to demonstrate the properties of hyperbolic spaces are: The Hyperboloid model, the Klein model, and the Poincare Disc Model. Despite its abstract nature, Hyperbolic spaces have been shown to have useful applications in art, biology, and theoretical physics. Main Discussion
I. History/Development of Hyperbolic Spaces
In order to understand something as complex as Hyperbolic Space, it is first important to understand what is not a Hyperbolic Space, Euclidean Space. Euclidean Space, while the name may be unfamiliar, the concept should be very familiar as it is the type of space we experience every day. The name comes from Euclid of Alexandria, also known as the “father of geometry”, who wrote 5 unproved axioms:
Table 1:
| 1 | Given two points there is one straight line that joins them. |
| 2 | A straight line segment can be prolonged indefinitely. |
| 3 | A circle can be constructed when a point for its center and a distance for its radius are given. |
| 4 | All right angles are equal. |
| 5 | If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than the two right angles. |
Note: (Taisbak & van der Waerden, Euclid 2019)
To most people these seem standard, and well accepted. The fifth one is a little more complicated, but really it just means that when two non-parallel lines are intersected there is a point where original two lines will meet and form a triangle. In broad terms it justifies that that the angles in a triangle add up to 180 degrees and the angles in a square add up to 360 degrees. Through High School the only type of space discussed is this flat, 2-dimensional one that follows all 5 of Euclid’s axioms, called Euclidean Space, however there is a branch of mathematics that studies Non-Euclidean Spaces. These are curved spaces where Euclid’s 5th axiom no longer applies. A positively curved space is called a spherical space, which you can find more information on at: https://bakingandmath.com/2014/10/02/what-is-hyperbolic-space/
She has great visualizations and does a good job explaining both spherical and hyperbolic spaces.
A negatively curved space is called a hyperbolic space, which due to its irregularities compared to Euclidean geometry has 4 main models to describe and model its complex hyperbolic geometry. It is important to note that none of these models are perfect. The problem of creating a flat map of the spherical world is that there is always going to be some kind of distortion. This applies to hyperbolic modeling as well; each model creates some kind of distortion.
II. Hyperboloid Model
This model is the basis of the Klein and Poincare Models. It is also called the Minkowski model after famous mathematician: Hermann Minkowski. It represents points in a hyperbolic space as a two sheeted hyperboloid. This is an incomplete representation as it focusses solely on the positive sheet of a two sheeted hyperboloid, however it makes visualization of the hyperbolic space possible.
III. Klein Model
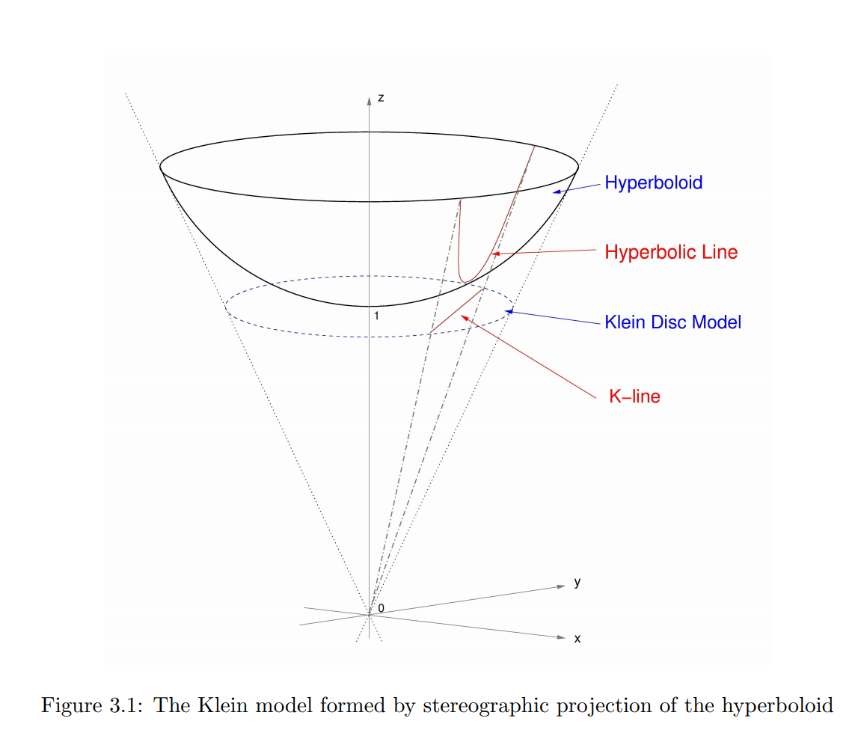
One of the main models for modeling hyperbolic space is the Belrami-Klein Model, also known as the projective model. In this model Euclid’s axiom 2 holds that says, “A straight line segment can be prolonged indefinitely”, but as a result it distorts angles and distances. This model is formed from an orthographic projection of a 3-dimensional hyperboloid onto the plane outlined by the Euclidean Unit Circle. This projection of a curved surface onto a plane as straight lines is called orthographic projection.
One way of thinking about this is to imagine looking up at a bowl where out at the largest diameter of the bowl it extends upward infinitely. This is a rough idea of what a two-sheet hyperboloid would look like from the origin. If you drew exactly what you saw without shading, a line that goes around the bottom of the bowl would be drawn as a straight line in a circle. Here is a diagram of this:
Note: (Hayter, The Hyperbolic Plane “A Strange New Universe" 2008)
The Klein disc that the hyperboloid is being projected on is a unit disc with radius 1, height 1, and centered at the origin. If the central projection is defined as f then
Note: This is the one-to-one projection of the hyperboloid onto the Klein Disc.
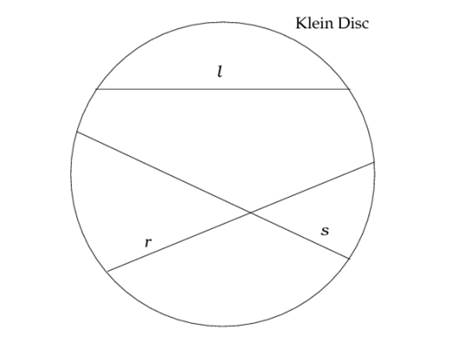
Since a hyperboloid extends upward to infinity, the distance across the Klein disc represents an infinite distance. In this model, parallel hyperbolic lines are lines that never cross in the Klein Disc. Some might think that s and r are not parallel to l in figure 3 as they would cross l is extended past the Klein Disc, but then it would no longer be in the hyperbolic plane that was projected onto the Klein Disc. Since the projections on the Klein Disc are straight lines, as shown in Figure 3, there is an axiom that states for any two points in the Klein Disc there exists only one open chord that goes through both points. This axiom is what makes it possible to measure distance in the Klein Model. The distance formula for the Klein-Beltrami Model is:
Note: P and Q are points in the model, while M and N are the endpoints of the chords, and PM, NQ, QM, and PN are Euclidean lengths
IV. Poincare Disc Model
Similar to the Klein model, the diameter of the disc is infinite. If a bug was on the surface of a hyperboloid and was following a line shown in the Poincare disc, then the set of legs of the bug closer to the origin would look larger than the set of legs closer to the edge of the disc. As the outside viewer the bug will look like it is shrinking as it goes away from the origin of the Poincare Disc, but from the bugs perspective it would remain the same size. From the bugs perspective it will be walking in a straight line, but from our perspective of the Poincare disc it will look like it was walking in a curve. In comparison to the Klein model that uses orthographic projection onto a disc, the Poincare Disc Model uses stereographic projection.
https://youtu.be/VX-0Laeczgk Figure 4: 
Note: This is a great, short video explain stereographic projection. (Segerman & Schleimer, 2015)
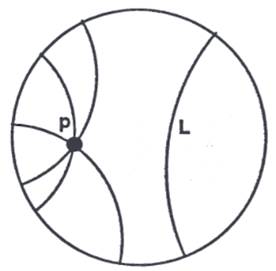
As shown in the video linked above and Figure 4, stereographic projection can project curved lines as straight lines in a plane. In the Poincare Disc Model, a similar but opposite thing occurs. The shortest distance between two points (straight lines) in hyperbolic space are projected onto the Poincare Disc as curved arcs of circles that are orthogonal to the boundary (intersect the boundary at right angles). There is an exception in the Poincare Model if one of the points is the origin. In this case, the distance is projected onto the Poincare Disc as a straight line.
Note: (Hayter, The Hyperbolic Plane “A Strange New Universe" 2008)
The distance between two points on the Poincare disc is defined by:
Equation 3: 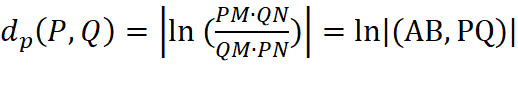
Note: P and Q are points in the Poincare Model, while M and N are the endpoints of the chords, PM, NQ, QM, and PN are Euclidean arclengths
An advantage of this model is that hyperbolic circles are displayed as circle on the Poincare Disc and Euclidean angles between the circles in the Poincare Disc are equivalent to the hyperbolic angles between the lines in the hyperbolic plane. This means the Poincare Model is conformal. One interesting feature of hyperbolic geometry eevident from the Poincare model is that the interior of angles of hyperbolic triangles approach 0 as their vertices approach infinity. A further explanation of this can be found at:
https://www.whitman.edu/documents/Academics/Mathematics/valaasla.pdf
It is also possible to have higher dimensional hyperbolic spaces. A Poincare model of a regular icosahedron in a hyperbolic space of 3 Dimensions is shown in Figure 6 compared to a regular icosahedron in Euclidean Space in Figure 7. IN Figure 6, the boundary sphere is a unit sphere, the lines are the intersections of the spheres that intersect the boundary orthogonally, and the faces are the portions of the faces of the spheres that intersect the boundary orthogonally.
Note: (Sander, Models of the Hyperbolic Plane 1996) (Regular icosahedron 2020)
V. Art Based on Models
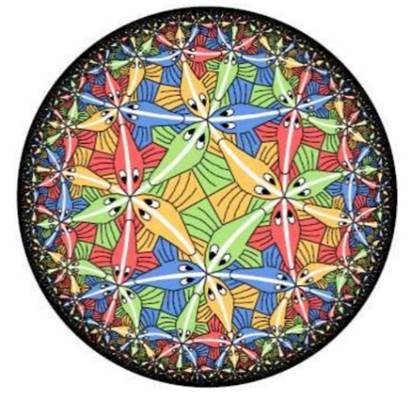
M.C. Escher is a Dutch, graphic artist from the early 20th century who was known for his geometric patterns and art based on mathematical principles. Escher was the first artist to create patterns in hyperbolic space. He used the Poincare Disk Model to create a repeating pattern with a circular limit as the Poincare Disk Model is bounded by the unit circle. His most well-known hyperbolic pattern is called Circle Limit III is pictured below:
Note: (Dunham, M.C. Escher’s Use of the Poincaré Models of Hyperbolic Geometry)
Another artistic way people have modelled Hyperbolic Space is through crocheting. Cornell University Mathematician, Daina Taimina was the creator of this idea of modelling hyperbolic space with yarn. This is a fascinating alternative to the previously paper or 2-dimensional models due to its robust nature and ability to be manipulated. Dr. Taimina’s modeling works are displayed in the Smithsonian’s collection of American Mathematical Models. Some examples of her work are shown below:
Note: (Hyperbolic Space Crochet Models) The yellow lines pictured in Figure 9 demonstrates how straight lines in Hyperbolic Space (also known as geodesics) look curved in Euclidean space as discussed in the Klein and Poincare Models. Figure 10 demonstrates the idea that in hyperbolic space the parallel postulate (Euclid’s 5th axiom) is violated because multiple straight lines can go through the same point and not intersect with an outside line.
VI. Applications and Further Readings
Previously, it was thought of that hyperbolic spaces had no application outside of theoretical math, but from a recent study done on the olfactory system, this may not be the case. The authors of this study discovered a way to map odors as point in a hyperbolic space. In their study they discuss how biological data is often represented by dendograms (hierarchal tree structures) and Venn Diagrams and how they found a way to connect these two diagrams by utilizing a 3-dimensional hyperbolic space. The study and an article analyzing and comparing this study with similar ideas are linked below:
https://advances.sciencemag.org/content/4/8/eaaq1458
Hyperbolic spaces have also been a foundational aspect of Einstein’s theory of relativity. It has also played a critical role in special relativity through a discussion of vectors in hyperbolic space called gyrovectors. If you want to learn more about the applications of the hyperbolic spaces in Einstein’s theory of relativity, I would suggest this article written by A. A. Unger as well the following written by William Ziemer. Both focus on the specifics of hyperbolic geometry in the theory of relativity. If very driven to understand this farther A. A. Unger wrote a book called “Analytic Hyperbolic Geometry and Albert Einstein’s Special Theory of Relativity”.
https://www.sciencedirect.com/science/article/pii/S0898122105000271 https://web.csulb.edu/~wziemer/Papers/specialrelativity.pdf
This is a link to an thought-provoking YouTube video done by Dick Canary explaining how being in hyperbolic space instead of Euclidean space would affect the sports of Baseball and Golf. It is not only an interesting concept to think about, it also is very helpful in understanding the many contradictory aspects of Hyperbolic Space compared to Euclidean Space.
This is a link to another YouTube video by the same authors as the one mentioned earlier to show stereographical projection. The do a great job explaining with visuals the different projections used in the Klein and Poincare Model. https://youtu.be/eGEQ_UuQtYs
References
Dunham, D. M.C. Escher’s Use of the Poincaré Models of Hyperbolic Geometry. http://www.math-art.eu/Documents/pdfs/Dunham.pdf
Hayter, R. (2008, April 20). The Hyperbolic Plane “A Strange New Universe". Retrieved December 04, 2020, from http://www.maths.dur.ac.uk/Ug/projects/highlights/CM3/Hayter_Hyperbolic_report.pdf
Hyperbolic Space Crochet Models. The Institute For Figuring. https://www.theiff.org/oexhibits/oe1e.html
Sander, E. (1996, June 18). Models of the Hyperbolic Plane. The Geometry Forum. http://www.geom.uiuc.edu/docs/forum/hype/model.html
Taisbak, C. M., & Van der Waerden, B. L. (2019, August 2). Euclid. Retrieved December 04, 2020, from https://www.britannica.com/biography/Euclid-Greek-mathematician
Segerman, H., & Schleimer, S. (2015, December 14). Illuminating hyperbolic geometry. YouTube. https://youtu.be/eGEQ_UuQtYs
Wikimedia Foundation. (2020, September 13). Regular icosahedron. Wikipedia. https://en.wikipedia.org/wiki/Regular_icosahedron