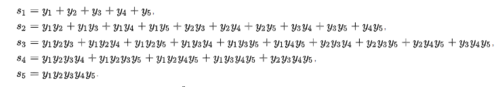Contents
Main Discussion
The Galois Group
Now that groups and fields have been described, it is time to define the Galois group.
For starters, define a group G. Referring back to field extensions, if there exists an extension F of Q, then there exists a grouping of automorphisms of Q onto F. Let the group G be the container of these automorphisms. In general, this basic definition is referred to as the Galois group of the field extension. However, if the field F is actually the splitting field of a polynomial, then it can be called the Galois group of that polynomial.
If the Galois group is a grouping of automorphisms of a field, then how can one know it is a group? What is its operation? A Galois group makes use of function composition as its operation, f * g, where f and g are members of the Galois group.
The notation of a Galois group involves using Gal(K), where K is an input. This can be denoted Gal(F/Q) if one is describing the Galois group of a field extension, and Gal(P) for a polynomial if P is a polynomial.
So, what's the purpose of such an abstractly defined structure? The answer to this question involves what a Galois group is capable of doing. For instance, if a Galois group is found for a polynomial p(x), and one proves that this Galois group is solvable over the radicals, then the polynomial has radical roots. This is an important idea for proving that general equations do not exist for polynomials of a certain degree as seen later in the Abel-Ruffini Theorem.
Abel-Ruffini Theorem
Polynomials of degree 1 to 4 have been studied and formulae to find their solutions have been described. However, polynomials of degree 5 and greater have been shown to not be solvable in the general sense. As a disclaimer, this does not mean that all polynomials of degree 5 or greater have no solution; a quintic equation x^5 - 1= 0 obviously has a solution of one. This result can be arrived at using Galois Theory. The entire proof of the general solvability of a polynomial of degree 5 or higher spans many pages of a typical print size and would be absolutely unreachable to an undergraduate student of reasonable mathematical knowledge. Thus, this section is dedicated to the application of Galois groups to proving this long standing question of mathematics, by looking at the major key points of a proof. The result of the larger proof is known as the Abel-Ruffini theorem.
In order to approach proving the general case of a polynomial of degree 5 or higher as unsolvable, one must prove that the Galois group of a polynomial p(x) of degree 5 or higher is an unsolvable group over the radicals. The Abel-Ruffini theorem is valid for fields of "characteristic 0." This is a condition that may be ignored for the purposes of this article, because it deals with the concept of a ring, an object used in Abstract Algebra.
For five numbers, y1,y2,y3,y4,y5, there exists a polynomial P(x) in a field E:
Then, expanding the polynomial, one obtains what is called a "symmetrical function":
One thing to note is that E is the splitting field of the polynomial. If one were to construct another field, called K, then K = Q(y1,y2,y3,y4,y5). Furthermore, S5 is a symmetric group that contains all the permutations of the five yi. The rest of the proof involves showing that S5 is not solvable and then showing that the Galois group is not solvable in the general case. Then, one may conclude that there does not exist a "general" solution to the polynomial of the fifth degree.
Fundamental Theorem Of Galois Theory
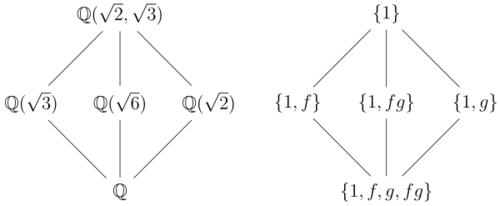
Another use of Galois groups is in the context of the fundamental theorem Of Galois theory, an aspect of Galois theory. The Fundamental Theorem of Galois theory involves one-to-one relations between intermediate fields within a greater Galois group. For a Galois group with a field extension K/F, there exists "intermediate" fields within the Galois group where for an intermediate field J there is the relation J/F and K/J. The relationship between J and other intermediate fields is always one-to-one.
Cyclic Group
Notice how cyclic groups were missing from the definition of the Galois group? The inclusion of cyclic groups in the group section was no mistake; they can arise from an interesting case of function composition with Galois groups. Consider a Galois group for the function x^2 - 5 = 0. Elements of this group take on the form a + b√5 and a function f that is part of the Galois group E causes f(a + b√5) = a - b√5. If one were to do this operation again, f(f(a + b√5)), then the answer would be a + b√5, a return to the original term. Consider another function g that is a member of E, where g(x) = x. Then f(f(x)) = g(x), causing a cyclical pattern. As a result of this, one can define a cyclical group C2 that is identical to G.
Constructability
The next section talks about the ability for Galois groups to help describe what is and is not constructible. Galois theory and the Galois group are famous for solving questions involving the unmarked straightedge and the compass and the ability to draw a geometric figure using them.
Example Problems
1. Write the Galois group for the polynomial x^2 - 3 in field extension notation
Solution: Gal(Q[√3]/Q)
The polynomial has roots of -√3 and √3. So the field extension can be written as an extension of the rational numbers, Q. Thus, one may write the field extension as Q[√2]/Q. The Galois group of this field extension is then Gal(Q[√3]/Q)
2. Write the Galois group for the polynomial x^4 - 7x^2 + 10
Solution: Gal(Q[√2, √5]/Q)
The polynomial has roots of -√2, √2, -√5, and √5. So the field extension can be written as an extension of the rational numbers, Q. Thus, one may write the field extension as Q[√2, √5]/Q. The Galois group of this field extension is then Gal(Q[√2, √5]/Q)
3. Write the general form of a member of a field with form Q[√6]
Solution: a + b√6, where a and b are rational numbers
4. Write the Galois group for the polynomial x6-10x4+31x2-30
Solution: Gal(Q[√2, √3, √5]/Q)
The polynomial has roots of -√2, √2, -√3, √3, -√5, and √5. So the field extension can be written as an extension of the rational numbers, Q. Thus, one may write the field extension as Q[√2, √3, √5]/Q. The Galois group of this field extension is then Gal(Q[√2, √3, √5]/Q)
5. Can a angle of 30 degrees be trisected by an unmarked straightedge and compass?
Solution: The next article discusses the solution to this problem.