| Line 51: | Line 51: | ||
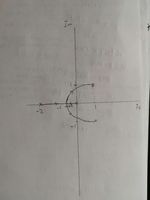
B) Two complex conjugate zeros: | B) Two complex conjugate zeros: | ||
| − | arrival angle of zero 1+j: angle to zeros <math>(1+j) - (1-j) = 90 \ | + | arrival angle of zero 1+j: angle to zeros <math>(1+j) - (1-j) = 90^{\circ} </math> |
==Problem 4== | ==Problem 4== | ||
Revision as of 23:28, 1 August 2019
Automatic Control (AC)
Question 1: Feedback Control Systems
August 2017 (Published in Jul 2019)
Contents
Problem 1
A) $ \frac{C(s)}{R(s)} = \frac{4}{s(s+1)} $
B) $ \frac{B(s)}{E(s)} = \frac{2}{s+1}+\frac{4}{s(s+1)} = \frac{2s+4}{s(s+1)} $
C) $ \frac{C(s)}{R(s)} = \frac{\frac{4}{s(s+1)}}{1+\frac{2s+4}{s(s+1)}} $
D) $ 1+\frac{2s+4}{s(s+1)} = 0 $
E) $ s(s+1)+2s+4 = 0 \Rightarrow s^2+3s+4=0 $
$ \therefore \omega_n^2 =4, \; 2\zeta \omega_n = 3 \Rightarrow \tau = \frac{1}{\zeta \omega_n} = \frac{3}{2} $
F) $ \frac{3}{4} $
G) since $ \zeta > 0 \therefore \omega_n = 2 $
H) two poles, type 2
I) $ \ddot{y}(t)+\dot{y}(t) = 4u(t) $
Problem 2
$ k_p = \lim_{s\rightarrow 0} G(s) = \infty $
$ k_v = \lim_{s\rightarrow 0} sG(s) = \frac{K}{6} $
$ e_ss = \lim_{s\rightarrow 0}sE(s) = \lim_{s\rightarrow 0} \frac{sR(s)}{1+G(s)} = \frac{1}{1+\lim_{s\rightarrow 0}G(s)} + \frac{1}{\lim_{s\rightarrow 0}sG(s)} = \frac{1}{1+k_p} + \frac{1}{k_v} = 0.2 $ $ \therefore K = 30 $
Problem 3
B) Two complex conjugate zeros:
arrival angle of zero 1+j: angle to zeros $ (1+j) - (1-j) = 90^{\circ} $