| Line 11: | Line 11: | ||
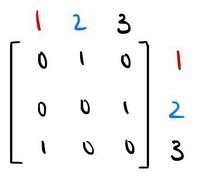
We can also write that in matrix form: | We can also write that in matrix form: | ||
| − | <center>[[File:Transitionmatrix2.jpg| | + | <center>[[File:Transitionmatrix2.jpg|200px|thumbnail]]</center> |
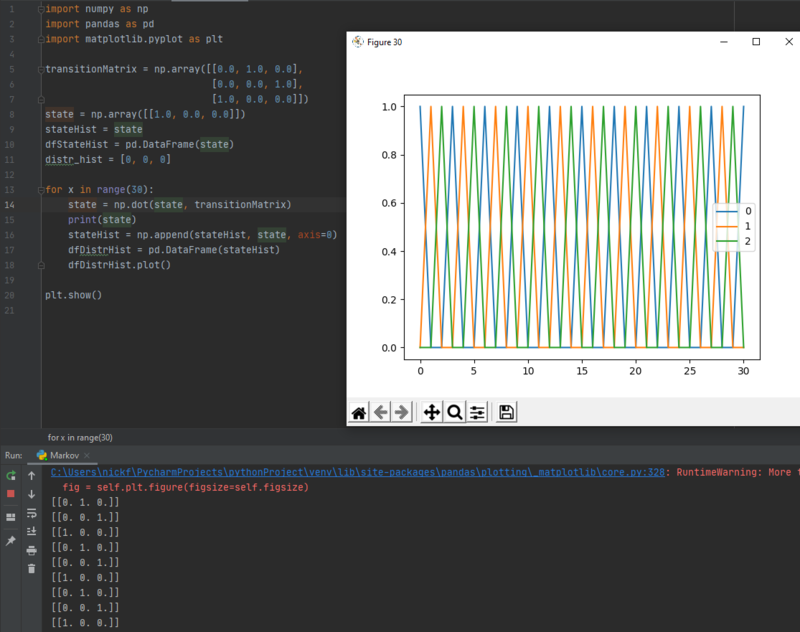
Going back to the Python program from before, when the initial state is <math>[1, 0, 0]</math>, | Going back to the Python program from before, when the initial state is <math>[1, 0, 0]</math>, | ||
| − | <center>[[File:Pythondemo7. | + | <center>[[File:Pythondemo7.png|800px|thumbnail]]</center> |
| + | |||
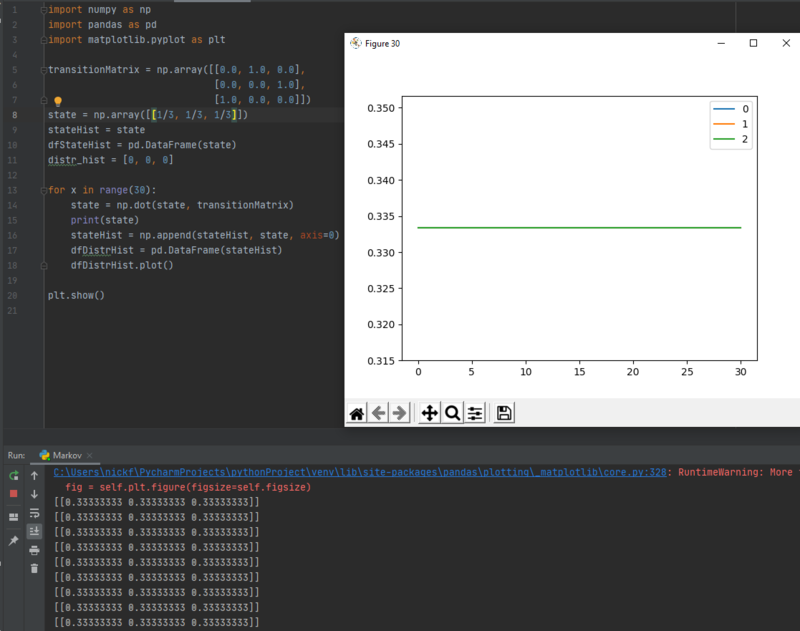
| + | When the initial state is <math>[\frac{1}{3}, \frac{1}{3}, \frac{1}{3}]</math>, while the transition probability matrix stays the same, the result looks like this: | ||
| + | |||
| + | <center>[[File:Pythondemo8.png|800px|thumbnail]]</center> | ||
| + | |||
| + | From this example, we know that: for a periodic Markov chain, the long-term distribution is dependent on the initial state vector. | ||
| + | |||
| + | Conducting similar experiments, we can reach a more general conclusion: any aperiodic and irreducible finite Markov chain has precisely one stationary distribution. Otherwise, there might be more than one stationary distribution or no stationary distribution at all. | ||
| + | |||
| + | Now, when referring to the Classification of States section to examine the weather example, we can see that the transition probability matrix for the weather example is indeed aperiodic and irreducible. Therefore we get one stationary distribution, as demonstrated above using python. | ||
| − | |||
[[ Walther MA271 Fall2020 topic2|Back to Markov Chains]] | [[ Walther MA271 Fall2020 topic2|Back to Markov Chains]] | ||
[[Category:MA271Fall2020Walther]] | [[Category:MA271Fall2020Walther]] | ||
Revision as of 03:39, 6 December 2020
=Restrictions of Stationary Distribution
In the last section, it is emphasized that steady-state vectors can be derived only with regular matrices. What if these vectors are not regular?
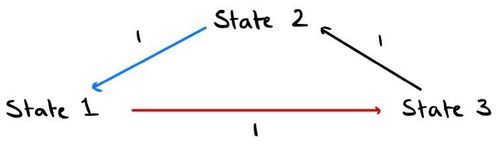
Consider a periodic Markov chain:
We can also write that in matrix form:
Going back to the Python program from before, when the initial state is $ [1, 0, 0] $,
When the initial state is $ [\frac{1}{3}, \frac{1}{3}, \frac{1}{3}] $, while the transition probability matrix stays the same, the result looks like this:
From this example, we know that: for a periodic Markov chain, the long-term distribution is dependent on the initial state vector.
Conducting similar experiments, we can reach a more general conclusion: any aperiodic and irreducible finite Markov chain has precisely one stationary distribution. Otherwise, there might be more than one stationary distribution or no stationary distribution at all.
Now, when referring to the Classification of States section to examine the weather example, we can see that the transition probability matrix for the weather example is indeed aperiodic and irreducible. Therefore we get one stationary distribution, as demonstrated above using python.