Parzen window method and classification
A slecture by ECE student Chiho Choi
Partly based on the ECE662 Spring 2014 lecture material of Prof. Mireille Boutin.
Contents
Density estimation using Parzen window
Unlike parametric density estimation methods, non-parametric approaches locally estimate density function by a small number of neighboring samples [3] and therefore show less accurate estimation results. In spite of their accuracy, however, the performance of classifiers designed using these estimates is very satisfactory.
The basic idea for estimating unknown density function is based on the fact that the probability $ P $ that a vector x belongs to a region $ R $ [1]:
It can be rewritten as
if we assume a small local region $ R $, a large number of samples $ n $, and $ k $ of $ n $ falling in $ R $.
Suppose that the region $ R $ is a $ d $-dimensional hypercube around $ \textbf{x}_i \in \mathbb{R}^n $ in the rest of this slecture, and let the volume $ V_n $:
where $ h_n $ is the length of an edge. Then the window function for this hypercube can be defined by
and displayed in Figure 1(a) and 1(b) below such cases where $ d $ = 1 and $ d $ = 2, respectively.
Figure 1. Given window function. (a) where $ d $ = 1, (b) where $ d $ = 2.
We simply shift this window function for $ \textbf{x}_i $ to determine if $ \textbf{x}_i $ belongs to the volume $ V_n $, $ \varphi(\frac{\textbf{x} - \textbf{x}_i}{h_n}) $, and can compute the number of samples $ k_n $ falling in this volume using it:
In Parzen window method, therefore, the estimate for density $ p_n(\textbf{x}) $ is
In order to check how window length effects on $ p_n(\textbf{x}) $, we define $ \delta_n(\textbf{x} - \textbf{x}_i) $ by $ \frac{1}{V_n} \varphi(\frac{\textbf{x} - \textbf{x}_i}{h_n}) $ as an approximation of a unit impulse centered at $ \textbf{x}_i $ [2] and write $ p_n(\textbf{x}) $ [1] by:
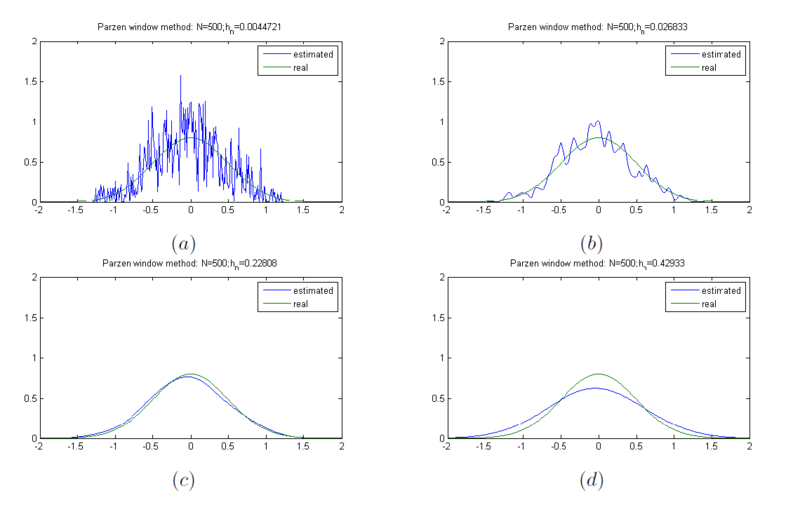
From this observation, we can infer the relationship between $ h_n $ and $ p_n(\textbf{x}) $. If $ h_n $ is very large, the amplitude of $ \delta_n $ is relatively small because $ V_n = h_n^d $. Thus, $ p_n(\textbf{x}) $ becomes a very smooth estimate for $ p(\textbf{x}) $ (see Figure 2(d)). In contrast, if $ h_n $ is very small, the amplitude of $ \delta_n $ is large. As a result, $ p_n(\textbf{x}) $ is a noisy estimate for $ p(\textbf{x}) $ (see Figure 2(a)). Therefore, when we have a limited number of samples, to find out an optimal value of $ h_n $ is very important to accurately estimate $ p(\textbf{x}) $. Let us assume that we have an unlimited number of samples. Then, $ V_n $ goes to zero as $ n $ increases, and hence $ p_n(\textbf{x}) $ converges to $ p(\textbf{x}) $ [1] no matter what $ h_n $ is.
Figure 2. Density estimate using Parzen window where N = 500. (a) $ h_n $ = 0.0044, (b) $ h_n $ = 0.0268, (c) $ h_n $ = 0.2280, and (d) $ h_n $ = 0.4293.
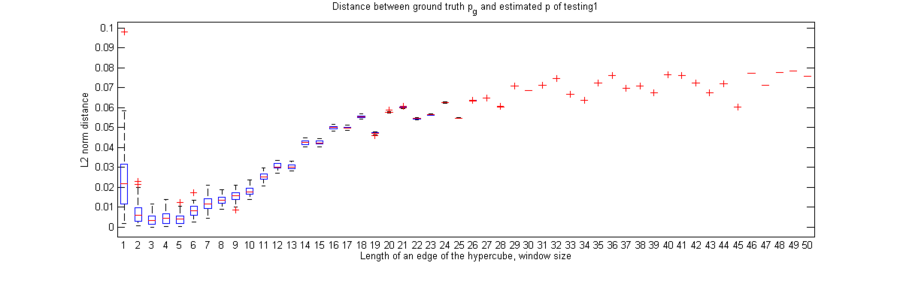
Figure 3. L2 norm distance between ground truth $ p $ and estimated $ p_n $.
In Figure 2, we can see the effect of the window length on the density estimate results. It demonstrates that a large or small $ h_n $ value causes inaccurate estimation for $ p(\textbf{x}) $. Also, as can be seen in Figure 3, the optimal window length in this experiment can be obtained around 3rd - 5th element ($ \textit{i.e.} $, $ h_n $ = 0.15 - 0.35) which shows minimum distance between ground truth $ p $ and estimated $ p_n $. As stated earlier, the choice of $ h_n $ is very important, especially when the number of samples is small.
Convergence of the mean and variance
Since x is a vector of random samples $ \textbf{x}_1, ..., \textbf{x}_n $, $ p_n $ has mean $ E(p_n(\textbf{x})) $ and variance $ Var(p_n(\textbf{x})) $. Thus, $ p_n(\textbf{x}) $ converges to $ p(\textbf{x}) $ [1], if
Let us prove the convergence of the mean and variance [2], respectively.
In order to make this formula converges to zero as $ n $ goes to infinity, according to the lecture note [2], we can make $ nV_n \rightarrow \infty $ and $ V_n\rightarrow 0 $ $ (\textit{e.g.}, V_n = \frac{1}{\sqrt{n}} $).
Classification using Parzen window method
A decision making using a classifier based on Parzen window estimation can be performed by simple majority voting method. Here, we check how it works. According to Professor Mireille Boutin [2], we pick the class such that $ Prob(w_{i0}|x_0) \geq Prob(w_i|x_0) \forall i=1,...,c $ from Bayes' rule. In other words,
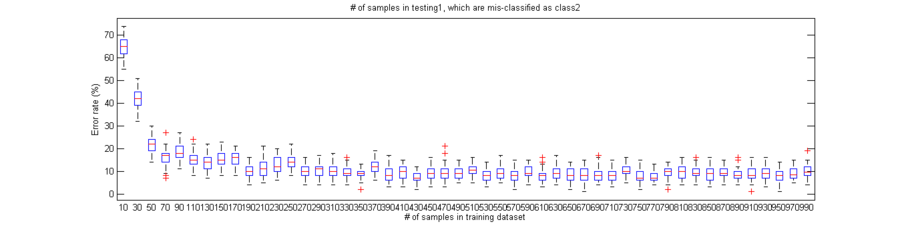
Figure 4. The classification error rates with respect to the number of samples from 10 to 1000.
We build a classifier using hypercube as a window function. Figure 4 illustrates the classification error rates with respect to the different number of samples while optimal window length obtained above is used. In this experiment, we can recognize that the error rate decreases as the number of samples in training dataset increases until it reaches about 190 samples. After that, the classification error rate seems stable no matter what the sample size is. It demonstrates that the performance of classifiers designed using this method is satisfactory, even though density estimation is not accurate with a small samples size. As mentioned earlier, this is one of the advantages of non-parametric approaches.
Discussion
So far, we analyzed one of the non-parametric methods, Parzen Window density estimation, focused on how to estimate density, how to converge to actual density, and how to generate a classifier using it. As we proved both theoretically and experimentally in this slecture, Parzen window shows super ability for decision making without any assumptions about the distributions of given sample data. However, finding an appropriate window function which would show better performance is going to be a tedious work, that is one of the disadvantages of Parzen window method.
References
[1] Pattern classification. Richard O. Duda, Peter E. Hart, and David G. Stork.
[2] Lecture notes of ECE 662, Professor Mireille Boutin.
[3] Introduction to Statistical Pattern Recognition. K. Fukunaga.
Questions and comments
If you have any questions, comments, etc. please post them on this page.