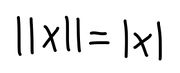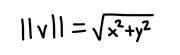Norms:
To understand the fundamentals of Banach Spaces, it is important to first visit the concept of norms. A norm is a function that represents vectors as scalars. It is primarily defined with three rules in mind: positive definiteness, absolute homogeneity, and triangle inequality.
Positive Definiteness:
Absolute Homogeneity:
For a scalar λ and vector x,
Triangle Inequality:
For vectors x and y,
Norms take different forms in different dimensions. In a 1 dimensional space, the norm of a vector is seen to be the absolute value of that vector. That is, for any vector x in one dimension,
In two dimensions, the norm of a vector is the square root of the sum of the squared x and y components of the vector. In other words, for a vector v defined by xi + yj,
The pattern continues into higher dimensions. In n-dimensional space, the norm of a vector is the square root of the sum of the squared dimensional components of the vector. For a vector v defined by (x1, …, xn),