Contents
RULES FOR CREATING PENROSE TILING
When creating a Penrose tiling, there are rules to keep in mind when arranging the tiles into their patterns. The exact specifications of these rules vary based on the type of tiles (discussed in the previous section), but ultimately, the tiles form an aperiodic pattern. How the tiles are arranged may also allow them to have reflectional or five-fold rotational symmetry.
KITE AND DART MATCHING
Recall the kite and dart, which are pieces of a rhombus that has angles of 72 and 108 degrees. There are different matching rules that ensure the tiles are put together in a form that does not have translational symmetry and thus ensures aperiodicity. For the kite and dart, there are two ways to join them.
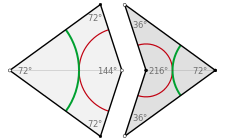
The first method is the vertex method. As previously described, the vertices along the kite’s axis of symmetry are labelled with one color. Then, the other two opposing vertices of the kite are labelled the other color. For the other shape, which is the dart, this is reversed. When joining the tiles together, only vertices of the same color may touch.
The other way of joining the kite and dart together is to draw two different colored arcs inside both shapes. Any two shapes that are joined together must create a smooth continuation of the arcs inside them, rather than any disjointed or broken lines.
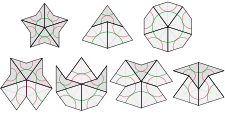
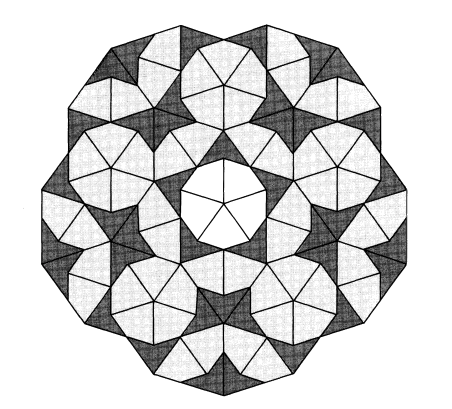
Using either of these two methods yields seven ways to fit the kite and dart around a point. The star shaped one and the sun enable five-fold rotational symmetry around the center. Patterns created using the five other starting tilings might have local five-fold symmetry at certain points in the pattern, but not throughout the whole tiling. Additionally, for all seven of these starting patterns, any local region found within the tiling will occur infinitely many times in the whole Penrose tiling. The seven originating arrangements can be seen in the figure below.
An example of a Penrose tiling using darts and kites can be seen below. This is the pavement of a central street in Helsinki, Poland.
RHOMBUS TILING
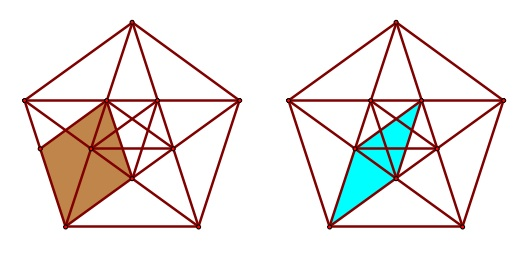
The next set of shapes is the two rhombi. Recall that these are created from splitting the kite and dart into triangles and then combining them into two rhombi, one thin and one thick. Interestingly, they can also be created from a regular pentagon using opposing triangles when a pentagram is inscribed into the pentagon and contains a smaller pentagon, also with a pentagram. The origin of the rhombi is shown below in the figure.
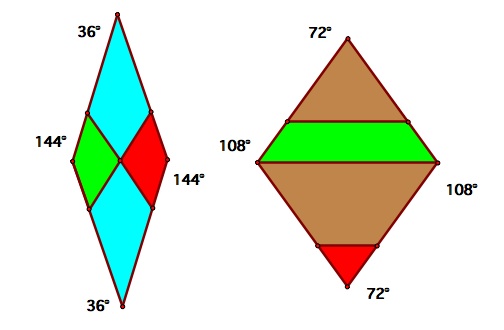
There are several ways of matching these rhombi into an aperiodic pattern. The overall rule is that the red portions of the rhombi may only touch other red pieces and the green pieces may only touch other green pieces. These portions are shown below.
An award-winning sculpture, called “Rhombi”, shows an example of this type of tiling.
CONTRADICTIONS
Simply following the aforementioned rules in one instance does not mean the pattern will create a perfect aperiodic tiling. For example, when adding kites and darts around one of the seven starting patterns discussed above, there are cases in which the choice of shape is “forced” -- that is, only one of the shapes can be put into a certain place. However, there are also many cases in which either a kite or a dart will work. Many times, choosing either one does not lead to an issue, but there can be instances where one prototile is chosen, and then when adding more pieces later on, a sort of dead end occurs, where no piece can be placed while following the rules of Penrose tilings.
In this situation, one may have to retrace their steps and change one of their choices such that the contradiction is eliminated. The more prototiles added on to the tiling, the more complex this becomes. Resolving a dead end may require changing several choices, and there is a wide array of possible combinations of choices that caused the contradiction that one must consider. Two of the starting patterns, the sun and the star, force the placement of every tile. A single, five-fold symmetrical pattern is created for both of these. Thus, no contradictions can occur when starting with those two tilings. The figure on the left below shows the sun pattern, and the one on the right shows the star (Gardner, 1988).