Line 27: Line 27:
 
where V is the volume of some neighborhood(say A) around x and k denotes the number of observations that are contained within the neighborhood.  
 
where V is the volume of some neighborhood(say A) around x and k denotes the number of observations that are contained within the neighborhood.  
 
The basic idea of k-NN is to extend the neighborhood, until the k nearest values are included. If we consider the neighborhood around x as a sphere, the volume of the sphere is given by,
 
The basic idea of k-NN is to extend the neighborhood, until the k nearest values are included. If we consider the neighborhood around x as a sphere, the volume of the sphere is given by,
−
<math> v_{k}(x_{0}) = \underset{h}{min}\left \{ \frac{\pi ^{n/2}.h^{n}}{\Gamma (\frac{n}{2} + 1)} \right \} </math>
+
<center><math> v_{k}(x_{0}) = \underset{h}{min}\left \{ \frac{\pi ^{n/2}.h^{n}}{\Gamma (\frac{n}{2} + 1)} \right \} </math></center>
  
 
where <math>\Gamma (n) = (n - 1)!</math>
 
where <math>\Gamma (n) = (n - 1)!</math>
Line 33: Line 33:
 
If x<sub>l</sub> is the k<sup>th</sup> closest sample point to x, then <math> h_{k} = \parallel x_{l} - x_{0}\parallel </math>
 
If x<sub>l</sub> is the k<sup>th</sup> closest sample point to x, then <math> h_{k} = \parallel x_{l} - x_{0}\parallel </math>
  
−
<math>v_{k}(x_{0}) =  \frac{\pi ^{n/2}}{\Gamma (\frac{n}{2} + 1)} . h_{k}^{n}</math>
+
<center><math>v_{k}(x_{0}) =  \frac{\pi ^{n/2}}{\Gamma (\frac{n}{2} + 1)} . h_{k}^{n}</math></center>
 +
 
 +
We approximate the density p(x) by,<br/>
 +
<center><math>\bar{\rho_{k}}(x_{0}) = \frac{k - \#s }{N.V_{k}(x_{0})}</math><br/></center>
  
−
We approximate the density p(x) by,<br/> <math>\bar{\rho_{k}}(x_{0}) = \frac{k - \#s }{N.V_{k}(x_{0})}</math><br/>
 
 
where #s is the number of samples on the boundary of circle wth radius h<sub>k</sub><br/>
 
where #s is the number of samples on the boundary of circle wth radius h<sub>k</sub><br/>
 
   
 
   
−
Most of the time this estimate is,<br/> <math>\bar{\rho_{k}}(x_{0}) = \frac{k - 1 }{N.V_{k}(x_{0})}</math><br/>
+
Most of the time this estimate is,<br/>
−
The Estimated density at x<sub>0</sub> is equal to the actual density x<sub>0</sub><br/><math>E(\bar{\rho_{k}}(x_{0})) = \rho(x_{0})</math>
+
<center><math>\bar{\rho_{k}}(x_{0}) = \frac{k - 1 }{N.V_{k}(x_{0})}</math><br/></center>
 +
The Estimated density at x<sub>0</sub> is equal to the actual density x<sub>0</sub><br/>
 +
<center><math>E(\bar{\rho_{k}}(x_{0})) = \rho(x_{0})</math></center>
  
 
We will now prove the above claim that the estimated density is also the actual density at x<sub>0</sub><br/>
 
We will now prove the above claim that the estimated density is also the actual density at x<sub>0</sub><br/>
Line 45: Line 49:
 
The above claim is true only in cases where the window function <math>\phi</math> defines a region R with well defined boundaries.That is, <br/>
 
The above claim is true only in cases where the window function <math>\phi</math> defines a region R with well defined boundaries.That is, <br/>
  
−
<math>\phi(x) = \begin{Bmatrix}1 , x \  \epsilon \ R  
+
<center><math>\phi(x) = \begin{Bmatrix}1 , x \  \epsilon \ R  
 
\\ 0, \ else
 
\\ 0, \ else
  
−
\end{Bmatrix}</math>
+
\end{Bmatrix}</math></center>
  
 
The random variable here is V<sub>k</sub>(x<sub>0</sub>)
 
The random variable here is V<sub>k</sub>(x<sub>0</sub>)
  
−
Let, <math>u = \int \rho(x)dx </math> where u is a small band along the boundary of R
+
Let,u be a small band along the boundary of R given by,
  
−
Observation : <math>u \epsilon [0,1]</math>
+
<center><math>u = \int \rho(x)dx </math></center>
  
−
Let G = event that "K-1 samples fall inside " <math>R</math> <br/>
+
<b>Observation : <math>u \epsilon [0,1]</math></b>
−
Let H = event that "1 sample falls inside the small band along the boundary" <br/>
+
 
 +
Let G be the event that "K-1 samples fall inside " <math>R</math>  
 +
and let H be the event that "1 sample falls inside the small band along the boundary" <br/>
  
 
Then, <br/>
 
Then, <br/>
−
<math>Prob(G, H) = Prob(G).Prob(H\mid G)</math> <br/>
+
<center><math>Prob(G, H) = Prob(G).Prob(H\mid G)</math> </center>
  
−
<math>Prob(G) = \binom{N}{K-1}u^{k-1}(1-u)^{N-K+1}</math><br/>
+
<center><math>Prob(G) = \binom{N}{K-1}u^{k-1}(1-u)^{N-K+1}</math></center>
  
−
<math>Prob(H\mid G) =  \binom{N-K+1}{1} \left ( \frac{\Delta u}{1-u} \right )\left ( 1 - \frac{\Delta u}{1-u} \right )^{N-K}</math><br/>
+
<center><math>Prob(H\mid G) =  \binom{N-K+1}{1} \left ( \frac{\Delta u}{1-u} \right )\left ( 1 - \frac{\Delta u}{1-u} \right )^{N-K}</math></center>
  
−
where <math>{\Delta u} = \int \rho(x)dx</math><br/>
+
where <math>{\Delta u} is given by,
 +
<center> <math>{\Delta u} = \int \rho(x)dx</math></center>
  
−
<math>Prob(G,H) = \binom{N}{K-1} \binom{N-K+1}{1} \left ( \frac{\Delta u}{1-u} \right ) u^{K-1}\left ( 1 - \frac{\Delta u}{1-u} \right )^{N-K}(1-u)^{N-K+1}</math><br/>
+
<center><math>Prob(G,H) = \binom{N}{K-1} \binom{N-K+1}{1} \left ( \frac{\Delta u}{1-u} \right ) u^{K-1}\left ( 1 - \frac{\Delta u}{1-u} \right )^{N-K}(1-u)^{N-K+1}</math></center>
  
−
<math>Prob(G,H) = \frac{N!}{1!(N-K+1)!}.\frac{N-K+1}{1!(N-K)!}</math><br/>
+
<center><math>Prob(G,H) = \frac{N!}{1!(N-K+1)!}.\frac{N-K+1}{1!(N-K)!}</math></center>
  
−
<math>Prob(G,H) = \frac{N!}{(k-1)!(N-K)!}.\Delta u(1 - u)^{N-K}u^{K-1}\left ( 1- \frac{\Delta u}{1-u}\right )^{N-K}</math><br/>
+
<center><math>Prob(G,H) = \frac{N!}{(k-1)!(N-K)!}.\Delta u(1 - u)^{N-K}u^{K-1}\left ( 1- \frac{\Delta u}{1-u}\right )^{N-K}</math></center>
  
−
<math>\left ( 1- \frac{\Delta u}{1-u}\right )^{N-K} = 1, when \  \Delta u \ is \ very \ small</math><br/>
+
<center><math>\left ( 1- \frac{\Delta u}{1-u}\right )^{N-K} = 1, when \  \Delta u \ is \ very \ small</math></center>
  
−
<math>Prob(G,H)\cong \Delta u. \frac{N!}{(k-1)!(N-K)!}.u^{k-1}(1-u)^{N-K}</math><br/>
+
<center><math>Prob(G,H)\cong \Delta u. \frac{N!}{(k-1)!(N-K)!}.u^{k-1}(1-u)^{N-K}</math></center>
  
−
So,<br/>
+
The Expected value of the density at x<sub>0</sub> by k-NN is given by,
−
<math> E(\bar{\rho }(x_{0})) = E(\frac{K-1}{N.V_{K}(x_{0})}) </math><br/>
+
<center><math> E(\bar{\rho }(x_{0})) = E(\frac{K-1}{N.V_{K}(x_{0})}) </math></center>
  
−
recall that<br/>, <math>u \cong \rho (x_{0}).V_{K}(x_{0})</math><br/>
+
recall that, <center><math>u \cong \rho (x_{0}).V_{K}(x_{0})</math></center>
  
−
<math>\Rightarrow V_{K}(x_{0}) = \frac{u}{\rho (x_{0})}</math><br/>
+
<center><math>\Rightarrow V_{K}(x_{0}) = \frac{u}{\rho (x_{0})}</math></center>
  
−
<math>E(\bar{\rho }(x_{0})) = E\left ( \frac{K-1}{N.u}.\rho (x_{0}) \right )</math><br/>
+
<center><math>E(\bar{\rho }(x_{0})) = E\left ( \frac{K-1}{N.u}.\rho (x_{0}) \right )</math></center>
  
−
<math>E(\bar{\rho }(x_{0})) = \frac{K-1}{N}\rho (x_{0}) E\left ( \frac{1}{u}\right)</math><br/>
+
<center><math>E(\bar{\rho }(x_{0})) = \frac{K-1}{N}\rho (x_{0}) E\left ( \frac{1}{u}\right)</math></center>
  
−
<math>E(\bar{\rho }(x_{0})) = \frac{K-1}{N}\rho (x_{0}) \int_{0}^{1}\frac{1}{u}\rho_{u}du</math><br/>
+
<center><math>E(\bar{\rho }(x_{0})) = \frac{K-1}{N}\rho (x_{0}) \int_{0}^{1}\frac{1}{u}\rho_{u}du</math></center>
  
−
<math>E(\bar{\rho }(x_{0})) = \frac{K-1}{N}\rho (x_{0}) \int_{0}^{1}\frac{1}{u}\frac{N!}{(K-1)!(N-K)!}u^{K-1}(1-u)^{N-K}du</math><br/>
+
<center><math>E(\bar{\rho }(x_{0})) = \frac{K-1}{N}\rho (x_{0}) \int_{0}^{1}\frac{1}{u}\frac{N!}{(K-1)!(N-K)!}u^{K-1}(1-u)^{N-K}du</math></center>
  
−
<math>E(\bar{\rho }(x_{0})) = \frac{K-1}{N}\rho (x_{0}) \int_{0}^{1}\frac{1}{u}\frac{N(N-1)!}{(K-1)(K-Z)!(N-K)!}u^{K-Z}(1-u)^{N-K}du</math><br/>
+
<center><math>E(\bar{\rho }(x_{0})) = \frac{K-1}{N}\rho (x_{0}) \int_{0}^{1}\frac{1}{u}\frac{N(N-1)!}{(K-1)(K-Z)!(N-K)!}u^{K-Z}(1-u)^{N-K}du</math></center>
  
−
<math>E(\bar{\rho }(x_{0})) = \frac{\rho (x_{0}).(N-1)!}{(K-Z)!}.\frac{1}{(N-K)!} \int_{0}^{1}u^{K-Z}(1-u)^{N-K}du</math><br/>
+
<center><math>E(\bar{\rho }(x_{0})) = \frac{\rho (x_{0}).(N-1)!}{(K-Z)!}.\frac{1}{(N-K)!} \int_{0}^{1}u^{K-Z}(1-u)^{N-K}du</math></center>
  
 
Now, <math> \int_{0}^{1}u^{K-Z}(1-u)^{N-K}du = \frac{\Gamma (k-1)\Gamma (N-K+1)}{\Gamma (N)} </math> and recall <math>\Gamma (n) = (n-1)!</math>. Substituting these in the above equation we get, <br/>
 
Now, <math> \int_{0}^{1}u^{K-Z}(1-u)^{N-K}du = \frac{\Gamma (k-1)\Gamma (N-K+1)}{\Gamma (N)} </math> and recall <math>\Gamma (n) = (n-1)!</math>. Substituting these in the above equation we get, <br/>
  
−
<math>E(\bar{\rho }(x_{0})) = \rho(x_{0})</math> as claimed.
+
<center><math>E(\bar{\rho }(x_{0})) = \rho(x_{0})</math>as claimed.</center>
  
 
== How to classify data using k-NN Density Estimate ==
 
== How to classify data using k-NN Density Estimate ==
−
Having seen how the density at a given point x is estimated based on the value of k and the given observations x<sub>1</sub>,x<sub>2</sub>,x<sub>3</sub>,...,x<sub>n</sub>, let's discuss about using the k-NN density estimate for classification. </br>
+
Having seen how the density at any given point x<sub>0</sub> is estimated based on the value of k and the given observations x<sub>1</sub>,x<sub>2</sub>,x<sub>3</sub>,...,x<sub>n</sub>, let's discuss about using the k-NN density estimate for classification. </br>
  
 
<b>Method 1:</b> <br/>
 
<b>Method 1:</b> <br/>
Line 110: Line 117:
 
Given are samples x<sub>i1</sub>,x<sub>x2</sub>,..,x<sub>xn</sub> for i classes. <br/>
 
Given are samples x<sub>i1</sub>,x<sub>x2</sub>,..,x<sub>xn</sub> for i classes. <br/>
  
−
We now pick a k<sub>i</sub> for each class and a window function, and we try to approximate the density at x<sub>0</sub> for each class and then pick the class with the largest density based on, <br/>
+
We now pick a k<sub>i</sub> for each class and a window function, and we try to approximate the density at x<sub>0</sub> for each class and then pick the class with the largest density based on,
  
−
<math>\rho(x_{0}\mid \omega _{i}) = \frac{k_{i} - 1 }{N_{i}.V_{k_{i}}(x_{0})}.Prob(\omega _{i})</math>
+
<center><math>\rho(x_{0}\mid \omega _{i}) = \frac{k_{i} - 1 }{N_{i}.V_{k_{i}}(x_{0})}.Prob(\omega _{i})</math></center>
  
 
If the priors of the classes are unknown, we use ROC curves to estimate the priors.
 
If the priors of the classes are unknown, we use ROC curves to estimate the priors.
Line 120: Line 127:
 
Given are samples x<sub>i1</sub>,x<sub>x2</sub>,..,x<sub>xn</sub> from a Gaussian Mixture. We choose a single value of k and and one window function, <br/>
 
Given are samples x<sub>i1</sub>,x<sub>x2</sub>,..,x<sub>xn</sub> from a Gaussian Mixture. We choose a single value of k and and one window function, <br/>
  
−
We then approximate the density at x<sub>0</sub> by, <br/>
+
We then approximate the density at x<sub>0</sub> by,
−
<math>\rho(x_{0}\mid \omega _{i}) = \frac{k_{i} - 1 }{N_{i}.V_{k_{i}}(x_{0})}</math></br>
+
<center><math>\rho(x_{0}\mid \omega _{i}) = \frac{k_{i} - 1 }{N_{i}.V_{k_{i}}(x_{0})}</math></center>
  
 
where V<sub>i</sub> is the volume of the smallest window that contains k samples and k<sub>i</sub> is the number of samples among these k that belongs to class i. <br/>
 
where V<sub>i</sub> is the volume of the smallest window that contains k samples and k<sub>i</sub> is the number of samples among these k that belongs to class i. <br/>
  
−
We pick a class i<sub>0</sub> such that,<br/>
+
We pick a class i<sub>0</sub> such that,
−
<math>Prob (\omega _{io}\mid x_{0})\geq Prob (\omega _{i}\mid x_{0}), \forall \ i = 1,2,..,c</math><br/>
+
<center><math>Prob (\omega _{io}\mid x_{0})\geq Prob (\omega _{i}\mid x_{0}), \forall \ i = 1,2,..,c</math></center>
−
<math>\Rightarrow \rho(x_{0}\mid \omega _{i0}).Prob (\omega _{io})\geq \rho(x_{0}\mid \omega _{i}).Prob (\omega _{i}), \forall \ i = 1,2,..,c</math><br/>
+
<center><math>\Rightarrow \rho(x_{0}\mid \omega _{i0}).Prob (\omega _{io})\geq \rho(x_{0}\mid \omega _{i}).Prob (\omega _{i}), \forall \ i = 1,2,..,c</math></center>
−
<math>\Rightarrow \rho(x_{0}, \omega _{i0}) \geq \rho(x_{0},\omega _{i}), \forall \ i = 1,2,..,c</math>
+
<center><math>\Rightarrow \rho(x_{0}, \omega _{i0}) \geq \rho(x_{0},\omega _{i}), \forall \ i = 1,2,..,c</math></center>
  
−
<math>k_{i0} \geq k_{i}, \forall \ i = 1,2,...,c</math>
+
<center><math>k_{i0} \geq k_{i}, \forall \ i = 1,2,...,c</math></center>
  
−
It boils down to assigning a class based on the majority vote of the k-nearest neighbors.
+
So classification using K-NN can also be thought as assigning a class based on the majority vote of the k-Nearest Neighbors at any point x<sub>0</sub>
  
−
== Computational Complexity ==
+
== Conclusion ==
−
 
+
−
k-NN Algorithm stores all the training data samples. Suppose we have n samples each of dimension k, k-NN takes,
+
−
<ul>
+
−
<li> O(d) time to calculate a single distance </li>
+
−
<li> O(nd) time to find one closest neighbor </li>
+
−
<li> O(knd) time to find k closest neighbors </li>
+
−
<li> Giving a total complexity of O(knd) </li>
+
−
</ul>
+
−
 
+
−
== Advantages and DisAdvantages of k-NN ==
+
  
 
K-NN is a simple and intuitive algorithm that can be applied to any kind of distribution. It gives a very good classification rate when the number of samples is large enough. But choosing the best "k" for the classifier may be difficult. The time and space complexity of the algorithm is very high, and we need to make several optimizations for efficiently running the algorithm.
 
K-NN is a simple and intuitive algorithm that can be applied to any kind of distribution. It gives a very good classification rate when the number of samples is large enough. But choosing the best "k" for the classifier may be difficult. The time and space complexity of the algorithm is very high, and we need to make several optimizations for efficiently running the algorithm.
Line 150: Line 147:
 
Neverthless, it's one among the most popular techniques used for classification.
 
Neverthless, it's one among the most popular techniques used for classification.
  
−
 
−
----
 
−
----
 
−
----
 
−
 
−
Post your slecture material here. Guidelines:
 
−
*If you are making a text slecture
 
−
**Type text using wikitext markup languages
 
−
**Type all equations using latex code between <nowiki> <math> </math> </nowiki> tags.
 
 
**You may include links to other [https://www.projectrhea.org/learning/about_Rhea.php Project Rhea] pages.  
 
**You may include links to other [https://www.projectrhea.org/learning/about_Rhea.php Project Rhea] pages.  
 
==[[slecture_title_of_slecture_review|Questions and comments]]==
 
==[[slecture_title_of_slecture_review|Questions and comments]]==

Revision as of 12:28, 30 April 2014


K-Nearest Neighbors Density Estimation

A slecture by CIT student Raj Praveen Selvaraj

Partly based on the ECE662 Spring 2014 lecture material of Prof. Mireille Boutin.

Introduction

This slecture discusses about the K-Nearest Neighbors(k-NN) approach to estimate the density of a given distribution. The approach of K-Nearest Neighbors is very popular in signal and image processing for clustering and classification of patterns. It is an non-parametric density estimation technique which lets the region volume be a function of the training data. We will discuss the basic principle behind the k-NN approach to estimate density at a point X and then move on to building a classifier using the k-NN Density estimate.

Basic Principle

The general formulation for density estimation states that, for N Observations x1,x2,x3,...,xn the density at a point x can be approximated by the following function,

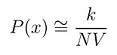
Knn1.jpg

where V is the volume of some neighborhood(say A) around x and k denotes the number of observations that are contained within the neighborhood. The basic idea of k-NN is to extend the neighborhood, until the k nearest values are included. If we consider the neighborhood around x as a sphere, the volume of the sphere is given by,

$ v_{k}(x_{0}) = \underset{h}{min}\left \{ \frac{\pi ^{n/2}.h^{n}}{\Gamma (\frac{n}{2} + 1)} \right \} $

where $ \Gamma (n) = (n - 1)! $

If xl is the kth closest sample point to x, then $ h_{k} = \parallel x_{l} - x_{0}\parallel $

$ v_{k}(x_{0}) = \frac{\pi ^{n/2}}{\Gamma (\frac{n}{2} + 1)} . h_{k}^{n} $

We approximate the density p(x) by,

$ \bar{\rho_{k}}(x_{0}) = \frac{k - \#s }{N.V_{k}(x_{0})} $

where #s is the number of samples on the boundary of circle wth radius hk

Most of the time this estimate is,

$ \bar{\rho_{k}}(x_{0}) = \frac{k - 1 }{N.V_{k}(x_{0})} $

The Estimated density at x0 is equal to the actual density x0

$ E(\bar{\rho_{k}}(x_{0})) = \rho(x_{0}) $

We will now prove the above claim that the estimated density is also the actual density at x0

The above claim is true only in cases where the window function $ \phi $ defines a region R with well defined boundaries.That is,

$ \phi(x) = \begin{Bmatrix}1 , x \ \epsilon \ R \\ 0, \ else \end{Bmatrix} $

The random variable here is Vk(x0)

Let,u be a small band along the boundary of R given by,

$ u = \int \rho(x)dx $

Observation : $ u \epsilon [0,1] $

Let G be the event that "K-1 samples fall inside " $ R $ and let H be the event that "1 sample falls inside the small band along the boundary"

Then,

$ Prob(G, H) = Prob(G).Prob(H\mid G) $
$ Prob(G) = \binom{N}{K-1}u^{k-1}(1-u)^{N-K+1} $
$ Prob(H\mid G) = \binom{N-K+1}{1} \left ( \frac{\Delta u}{1-u} \right )\left ( 1 - \frac{\Delta u}{1-u} \right )^{N-K} $

where $ {\Delta u} is given by, <center> <math>{\Delta u} = \int \rho(x)dx $</center>

$ Prob(G,H) = \binom{N}{K-1} \binom{N-K+1}{1} \left ( \frac{\Delta u}{1-u} \right ) u^{K-1}\left ( 1 - \frac{\Delta u}{1-u} \right )^{N-K}(1-u)^{N-K+1} $
$ Prob(G,H) = \frac{N!}{1!(N-K+1)!}.\frac{N-K+1}{1!(N-K)!} $
$ Prob(G,H) = \frac{N!}{(k-1)!(N-K)!}.\Delta u(1 - u)^{N-K}u^{K-1}\left ( 1- \frac{\Delta u}{1-u}\right )^{N-K} $
$ \left ( 1- \frac{\Delta u}{1-u}\right )^{N-K} = 1, when \ \Delta u \ is \ very \ small $
$ Prob(G,H)\cong \Delta u. \frac{N!}{(k-1)!(N-K)!}.u^{k-1}(1-u)^{N-K} $

The Expected value of the density at x0 by k-NN is given by,

$ E(\bar{\rho }(x_{0})) = E(\frac{K-1}{N.V_{K}(x_{0})}) $
recall that,
$ u \cong \rho (x_{0}).V_{K}(x_{0}) $
$ \Rightarrow V_{K}(x_{0}) = \frac{u}{\rho (x_{0})} $
$ E(\bar{\rho }(x_{0})) = E\left ( \frac{K-1}{N.u}.\rho (x_{0}) \right ) $
$ E(\bar{\rho }(x_{0})) = \frac{K-1}{N}\rho (x_{0}) E\left ( \frac{1}{u}\right) $
$ E(\bar{\rho }(x_{0})) = \frac{K-1}{N}\rho (x_{0}) \int_{0}^{1}\frac{1}{u}\rho_{u}du $
$ E(\bar{\rho }(x_{0})) = \frac{K-1}{N}\rho (x_{0}) \int_{0}^{1}\frac{1}{u}\frac{N!}{(K-1)!(N-K)!}u^{K-1}(1-u)^{N-K}du $
$ E(\bar{\rho }(x_{0})) = \frac{K-1}{N}\rho (x_{0}) \int_{0}^{1}\frac{1}{u}\frac{N(N-1)!}{(K-1)(K-Z)!(N-K)!}u^{K-Z}(1-u)^{N-K}du $
$ E(\bar{\rho }(x_{0})) = \frac{\rho (x_{0}).(N-1)!}{(K-Z)!}.\frac{1}{(N-K)!} \int_{0}^{1}u^{K-Z}(1-u)^{N-K}du $

Now, $ \int_{0}^{1}u^{K-Z}(1-u)^{N-K}du = \frac{\Gamma (k-1)\Gamma (N-K+1)}{\Gamma (N)} $ and recall $ \Gamma (n) = (n-1)! $. Substituting these in the above equation we get,

$ E(\bar{\rho }(x_{0})) = \rho(x_{0}) $as claimed.

How to classify data using k-NN Density Estimate

Having seen how the density at any given point x0 is estimated based on the value of k and the given observations x1,x2,x3,...,xn, let's discuss about using the k-NN density estimate for classification. </br>

Method 1:

Let x0 from Rn be a point to classify.

Given are samples xi1,xx2,..,xxn for i classes.

We now pick a ki for each class and a window function, and we try to approximate the density at x0 for each class and then pick the class with the largest density based on,

$ \rho(x_{0}\mid \omega _{i}) = \frac{k_{i} - 1 }{N_{i}.V_{k_{i}}(x_{0})}.Prob(\omega _{i}) $

If the priors of the classes are unknown, we use ROC curves to estimate the priors.

Method 2: </br>

Given are samples xi1,xx2,..,xxn from a Gaussian Mixture. We choose a single value of k and and one window function,

We then approximate the density at x0 by,

$ \rho(x_{0}\mid \omega _{i}) = \frac{k_{i} - 1 }{N_{i}.V_{k_{i}}(x_{0})} $

where Vi is the volume of the smallest window that contains k samples and ki is the number of samples among these k that belongs to class i.

We pick a class i0 such that,

$ Prob (\omega _{io}\mid x_{0})\geq Prob (\omega _{i}\mid x_{0}), \forall \ i = 1,2,..,c $
$ \Rightarrow \rho(x_{0}\mid \omega _{i0}).Prob (\omega _{io})\geq \rho(x_{0}\mid \omega _{i}).Prob (\omega _{i}), \forall \ i = 1,2,..,c $
$ \Rightarrow \rho(x_{0}, \omega _{i0}) \geq \rho(x_{0},\omega _{i}), \forall \ i = 1,2,..,c $
$ k_{i0} \geq k_{i}, \forall \ i = 1,2,...,c $

So classification using K-NN can also be thought as assigning a class based on the majority vote of the k-Nearest Neighbors at any point x0

Conclusion

K-NN is a simple and intuitive algorithm that can be applied to any kind of distribution. It gives a very good classification rate when the number of samples is large enough. But choosing the best "k" for the classifier may be difficult. The time and space complexity of the algorithm is very high, and we need to make several optimizations for efficiently running the algorithm.

Neverthless, it's one among the most popular techniques used for classification.

Questions and comments

If you have any questions, comments, etc. please post them on this page.

Back to ECE662, Spring 2014

Retrieved from "https://www.projectrhea.org/rhea/index.php?title=KnnDensityEstimation&oldid=64189"
Shortcuts
Help Main Wiki Page Random Page Special Pages Log in
Search

Alumni Liaison

Basic linear algebra uncovers and clarifies very important geometry and algebra.

Dr. Paul Garrett