Contents
Homework 5 Solution, ECE438, Fall 2015, Prof. Boutin
Plots in Solution
The plots were generated using this code.
Question 1
Downsampling and upsampling
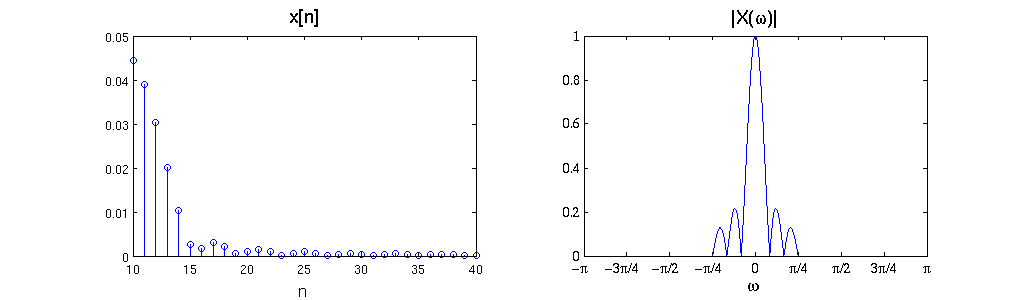
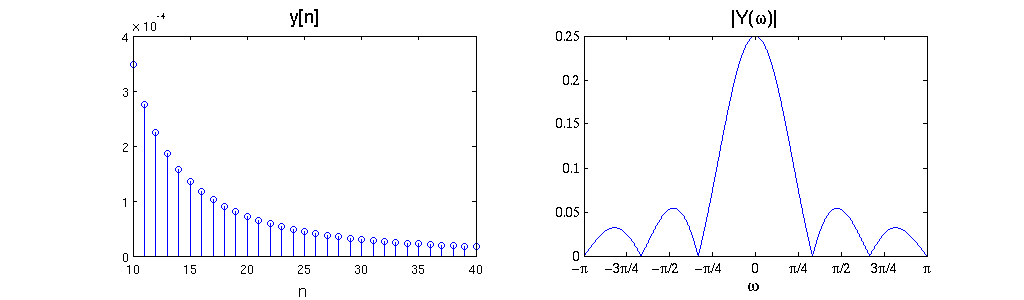
a) What is the relationship between the DT Fourier transform of x[n] and that of y[n]=x[4n]? (Give the mathematical relation and sketch an example.)
Solution
$ \mathcal{Y}(\omega) =\frac{1}{4} \sum_{k=0}^{3} \mathcal{X} \left (\frac{\omega-k2\pi}{4} \right ) $
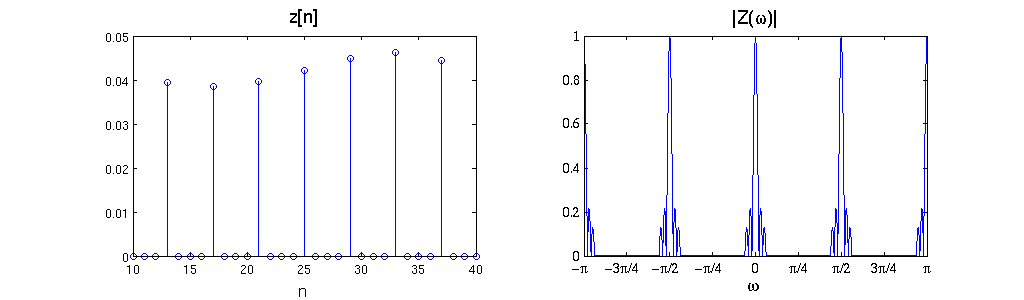
b) What is the relationship between the DT Fourier transform of x[n] and that of
$ z[n]=\left\{ \begin{array}{ll} x[n/4],& \text{ if } n \text{ is a multiple of } 4,\\ 0, & \text{ else}. \end{array}\right. $
(Give the mathematical relation and sketch an example.)
Solution
$ \mathcal{Z}(\omega) = \mathcal{X}(4\omega) $
Question 2
Downsampling and upsampling
Let $ x_1[n]=x(Tn) $ be a sampling of a CT signal $ x(t) $. Let D be a positive integer.
a) Under what circumstances is the downsampling $ x_D [n]= x_1 [Dn] $ equivalent to a resampling of the signal with a new period equal to DT (i.e. $ x_D [n]= x(DT n) $)?
Solution
All the time! Downsampling is always equivalent to resampling with a larger period.
b) Under what circumstances is it possible to construct the sampling $ x_3[n]= x(\frac{T}{D} n) $ directly from $ x_1[n] $ (without reconstructing x(t))?
Solution
As long as the original signal was sampled above the Nyquist rate, the upsampled signal, $ x_3[n] $, can be constructed directly from $ x_1[n] $.
Question 3
Define System 1 as the following LTI system
$ x(t)\rightarrow \left[ \begin{array}{c} \text{ LPF} \\ \text{ no gain} \\ \text{cutoff at 1000Hz} \end{array}\right] \rightarrow \left[ \begin{array}{ccc} & & \\ & H(f) & \\ & & \end{array}\right] \rightarrow y(t) $
where the frequency response H(f) corresponds to a band-pass filter with no gain and cutoff frequencies f1=200Hz and f2=600Hz.
a) Sketch the graph of the frequency response H(f) of System 1.
b) Sketch the graph of the frequency response $ H_1(\omega) $ that would make the following system equivalent to System 1.
$ x(t) \rightarrow \left[ \begin{array}{c} \text{LPF} \\ \text{ no gain }\\ \text{ cutoff at 1000Hz} \end{array}\right] \rightarrow \left[ \begin{array}{c} \text{C/D Converter} \\ \text{6000 samples per second} \end{array}\right] \rightarrow \left[ \begin{array}{c} H_1(\omega) \end{array}\right] \rightarrow \left[ \begin{array}{c} \text{D/C Converter} \\ \text{6000 samples per second} \end{array}\right] \rightarrow y(t) $
Solution
Note that the cutoff points for second filter, $ H_1(\omega) $, were found using $ w_0=(f_0/f_s)2\pi $.
Question 4
Define System 2 as the following LTI system
$ x[n]\rightarrow \left[ \begin{array}{ccc} & & \\ & H_1(\omega) & \\ & & \end{array}\right] \rightarrow y[n] $
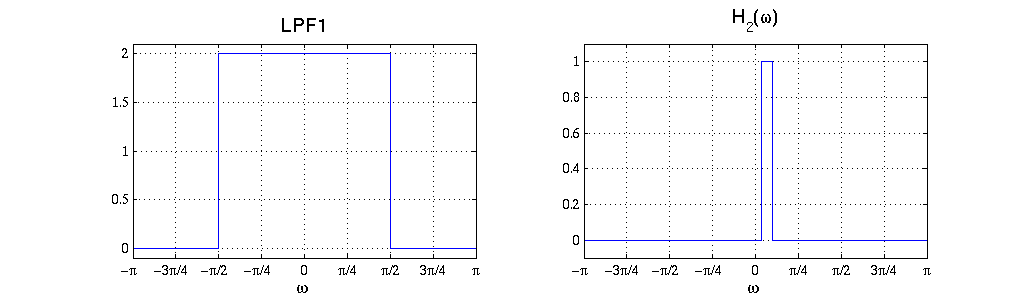
where the frequency response $ H_1(\omega) $ is the one you obtained in Question 3. Is it possible to implement System 2 as follows? Answer yes/no. If you answered yes, sketch the graph of the required LPF1 and frequency response H2. If you answered no, explain why not. (Hint: the first two parts of the system correspond to an "interpolator".)
$ x[n] \rightarrow \left[ \begin{array}{ccc} & & \\ & \text{Upsample by factor 2} & \\ & & \end{array}\right] \rightarrow \left[ \begin{array}{ccc} & & \\ & \text{LPF1 } & \\ & & \end{array}\right] \rightarrow \left[ \begin{array}{ccc} & & \\ & H_2(\omega) & \\ & & \end{array}\right] \rightarrow \left[ \begin{array}{ccc} & & \\ & \text{Downsample by factor 2} & \\ & & \end{array}\right] \rightarrow y([n] $
Solution
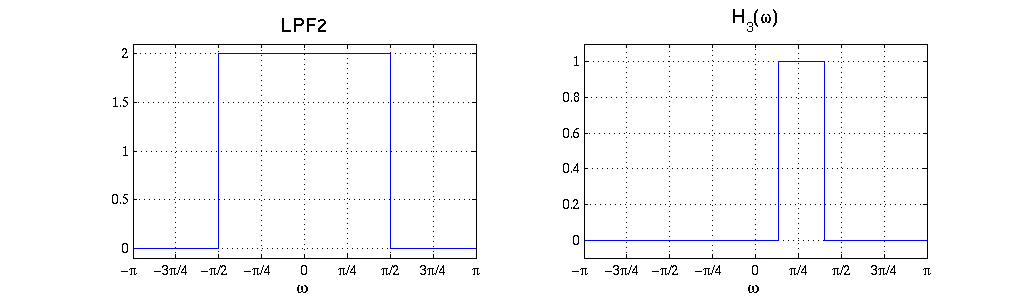
The standard interpolation filter to use for a factor L is $ H_L(\omega)=\begin{cases}L & \text{ for } |\omega|<\pi/L \\ 0 & \text{ for } \pi/L < |\omega| <\pi \end{cases} $. The cutoff frequencies for $ H_3(\omega) $ are found the same way as question 3, but now the effective sampling rate is 12000Hz.
Question 5
Define System 3 as the following LTI system
$ x[n] \rightarrow \left[ \begin{array}{c} \text{LPF} \\ \text{ no gain }\\ \text{ cutoff at} \frac{\pi}{2} \end{array}\right] \rightarrow \left[ \begin{array}{ccc} & & \\ & H_1(\omega) & \\ & & \end{array}\right] \rightarrow y[n] $
where the frequency response $ H_1(\omega) $ is the one you obtained in Question 3.
a) Is it possible to implement System 3 as follows? Answer yes/no. If you answered yes, sketch the graph of the required LPF2 and frequency response H3. If you answered no, explain why not. (Hint: the last two parts of the system correspond to an "interpolator".)
$ x[n] \rightarrow \left[ \begin{array}{c} \text{LPF} \\ \text{ no gain }\\ \text{ cutoff at} \frac{\pi}{2} \end{array}\right] \rightarrow \left[ \begin{array}{ccc} & & \\ & \text{Downsample by factor 2} & \\ & & \end{array}\right] \rightarrow \left[ \begin{array}{ccc} & & \\ & H_3(\omega) & \\ & & \end{array}\right] \rightarrow \left[ \begin{array}{ccc} & & \\ & \text{Upsample by factor 2} & \\ & & \end{array}\right] \rightarrow \left[ \begin{array}{c} \text{LPF2} \end{array}\right] \rightarrow y([n] $
Solution
Yes, it is possible. The Nyquist rate for the signal is 2000Hz (because of the first low-pass filter with cutoff at 1000Hz). After downsampling by 2, the effective sampling rate is 3000Hz, which is still above Nyquist. Therefore, there is no aliasing or loss of information, and the same filter can be designed with a sampling rate of 3000Hz.