Contents
Complex Number Basics (HW1, ECE301, Fall 2008)
I have the worst problem remembering Euler's Formula and working with it.
First here is the formula:
Euler's Formula
- $ \,\mathrm{e}^{j x} = (\cos x + j\sin x )\, $
Then relating it to the complex number plane:
Complex plane
Therefore finding :$ \,\mathrm{e}^{(j*pi)/2} = (\cos (pi/2) + j\sin (pi/2) ) = j\, $
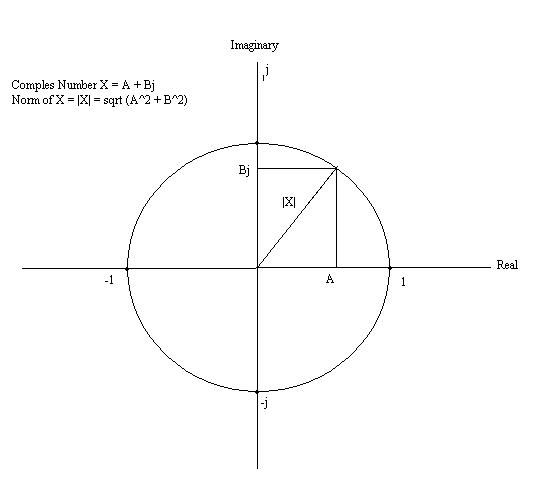
Finding the Norm of a complex number
The complex number is a vector with two parts; a real and an imaginary. Therefore finding the norm is like finding the magnitude of the vector.
If we have complex number X = A + Bj, where A is the real part and B is the imaginary part.
Then the norm (and magnitude) would be:
- $ \|\mathbf{x}\| := \sqrt{A^2 + B^2}. $
Finding the complex conjugate
The complex conjugate of a complex number is a simple matter of changing the sign on the imaginary part of the number. This is useful when you need to remove the imaginary part of the number from the denominator of your equation.
For example: X = A + Bj then the conjugate would be: Y = A - Bj
So if you have the equation: Z = 1 / (A + Bj)\
then you multiply by (A - Bj)/(A -Bj) and you get:
Z = (A - Bj)/(A^2 + B^2) as your new equation.
Back to ECE301 Fall 2008 Prof. Boutin