Answers and Discussions for
Contents
Problem 1
Create and Solve Magnetic Equivalent Circuit
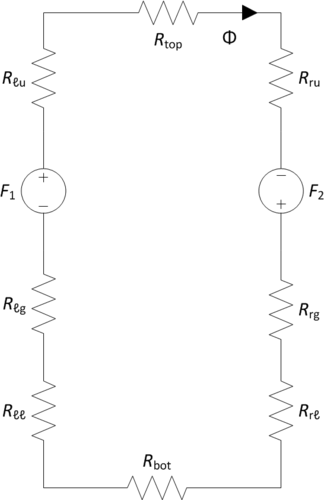
A magnetic equivalent circuit (MEC) needs to be constructed from the given UU core inductor geometry. A magnetomotive force (MMF) with general form $ \mathcal{F} = Ni $ acts as an analogue of an independent voltage source. In general, a reluctance may be expressed as $ \mathcal{R} = \frac{\ell}{\mu A} $ and function as a resistance analogue. If the steel has high permeability, then the reluctance associated with a path through steel is small (real conductor equivalent). In this problem, the permeability of air (linear, isotropic, and homogeneous) is treated as free space: $ \mu_{\text{air}} = \mu_{r,\text{air}} \mu_0 \approx \mu_0 $. Without any fringing or leakage considered, magnetic flux $ \Phi $ will more or less follow the direction of the steel.
The magnetomotive forces are straightforward expressions of turn count and current.
- $ \mathcal{F}_1 = Ni_1 $
- $ \mathcal{F}_2 = Ni_2 $
The reluctances need to be calculated using the length and cross sectional area presented to each path in their respective materials.
- $ \mathcal{R}_{\ell u} = \frac{d_s + \frac{1}{2}d_u}{\mu_r \mu_0 w_u \ell} = \mathcal{R}_{r u} = \mathcal{R}_{\ell \ell} = \mathcal{R}_{r \ell} $
- $ \mathcal{R}_{top} = \frac{w_s + w_u}{\mu_r \mu_0 d_u \ell} = \mathcal{R}_{bot} $
- $ \mathcal{R}_g(g) = \frac{g}{\mu_0 w_u \ell} $
The total magnetic flux passing through $ \mathcal{F}_1 $ and $ \mathcal{F}_2 $ needs to be found. It should be apparent that all reluctances are in series and thus add together to form the equivalent reluctance. A similar statement can be made for the equivalent MMF.
$ \begin{align} \Phi(i_1,i_2,g) &= \frac{\mathcal{F}_{eq}}{\mathcal{R}_{eq}} \\ \Phi(i_1,i_2,g) &= \frac{\mathcal{F}_1 + \mathcal{F}_2}{4\mathcal{R}_{\ell u} + 2\mathcal{R}_{top} + 2\mathcal{R}_g} \\ \Phi(i_1,i_2,g) &= \frac{Ni_1 + Ni_2}{4\frac{d_s + \frac{1}{2}d_u}{\mu_r \mu_0 w_u \ell} + 2\frac{w_s + w_u}{\mu_r \mu_0 d_u \ell} + 2\frac{g}{\mu_0 w_u \ell}} \\ \Phi(i_1,i_2,g) &= \frac{N (i_1 + i_2)}{\frac{2}{\mu_0 \ell} \left(\frac{2d_s + d_u}{\mu_r w_u} + \frac{w_s + w_u}{\mu_r d_u} + \frac{g}{w_u}\right)} \\ \Phi(i_1,i_2,g) &= \frac{N \mu_0 \ell (i_1 + i_2)}{2} \left[\frac{d_u (2d_s + d_u) + w_u (w_s + w_u) + \mu_r d_u g}{\mu_r w_u d_u}\right]^{-1} \\ \Phi(i_1,i_2,g) &= \frac{1}{2}N \mu_0 \ell (i_1 + i_2) \frac{\mu_r w_u d_u}{2 d_s d_u + d_u^2 + w_s w_u + w_u^2 + \mu_r d_u g} \\ \Phi(i_1,i_2,g) &= \frac{1}{2}N \mu_0 \ell (i_1 + i_2) G(g) \end{align} $
The magnetic flux from the MEC is compacted if the definition $ G_(g) \triangleq \frac{\mu_r w_u d_u}{2 d_s d_u + d_u^2 + w_s w_u + w_u^2 + \mu_r d_u g} $ is accepted. The magnetic flux linkage of the coils follow readily.
$ \begin{align} \lambda_1(i_1,i_2,g) &= N \Phi(i_1,i_2,g) \\ \lambda_1(i_1,i_2,g) &= \frac{1}{2}N^2 \mu_0 \ell (i_1 + i_2) G(g) \\ \lambda_2(i_1,i_2,g) &= \lambda_1(i_1,i_2,g) \end{align} $
Coenergy Calculation
Coenergy will be calculated in steps using a sequential ramping process. Before any steps can be completed, the contribution to coenergy of fixing the mechanical system should be documented (zero unless the mechanical system can store energy itself by moving from one position to another).
$ \begin{equation} W_{c,0} = 0 \end{equation} $
The first step in the coenergy calculation will ramp dummy variable $ i_1' $ from $ 0 $ to its final value of $ i_1 $ while dummy variable $ i_2' = 0 $ is held at its initial value.
$ \begin{align} W_{c,1} &= \int_{i_1' = 0}^{i_1} \left.\lambda_1\left(i_1', i_2', g\right) \, di_1'\right|_{i_2' = 0} + \int_{i_1' = 0}^{i} \left.\lambda_2\left(i_1', i_2', g\right) \, di_1'\right|_{i_2' = 0} \\ W_{c,1} &= 2\int_{i_1' = 0}^{i_1} \left.\lambda_1\left(i_1', i_2', g\right) \, di_1'\right|_{i_2' = 0} \\ W_{c,1} &= 2\int_{i_1' = 0}^{i_1} \frac{1}{2}N^2 \mu_0 \ell (i_1' + \cancelto{0}{i_2'}) G(g) \, di_1' \\ W_{c,1} &= N^2 \mu_0 \ell \left(\frac{1}{2} i_1^2\right) G(g) \end{align} $
The second step in the coenergy calculation will ramp dummy variable $ i_2' $ from $ 0 $ to its final value of $ i_2 $ while dummy variable $ i_1' = i_1 $ is held at its final value.
$ \begin{align} W_{c,2} &= 2\int_{i_2' = 0}^{i_2} \left.\lambda_1\left(i_1', i_2', g\right) \, di_2'\right|_{i_1' = i_1} \\ W_{c,2} &= 2\int_{i_2' = 0}^{i_2} \frac{1}{2}N^2 \mu_0 \ell (i_1 + i_2') G(g) \, di_2' \\ W_{c,2} &= N^2 \mu_0 \ell \left(i_1 i_2 + \frac{1}{2} i_1^2\right) G(g) \end{align} $
The final step is the sum all the individual coenergy contributions $ W_c(i_1, i_2, g) = \sum_{k = 0}^{2} W_{c,k}(i_1, i_2, g) $.
$ \begin{align} W_c(i_1, i_2, g) &= W_{c,0} + W_{c,1} + W_{c,2} \\ W_c(i_1, i_2, g) &= 0 + N^2 \mu_0 \ell \left(\frac{1}{2} i_1^2\right) G(g) + N^2 \mu_0 \ell \left(i_1 i_2 + \frac{1}{2} i_1^2\right) G(g) \\ W_c(i_1, i_2, g) &= N^2 \mu_0 \ell \left(\frac{1}{2} i_1^2 + i_1 i_2 + \frac{1}{2} i_2^2\right) G(g) \end{align} $
This calculation is consistent with the known result of a magnetically linear system having a coenergy of $ W_c(i_1, i_2, g) = \frac{1}{2} L_{11}(g) i_1^2 + L_{12}(g) i_1 i_2 + \frac{1}{2} L_{22}(g) i_2^2 = \frac{1}{2} \sum_{j = 1}^2 \sum_{k = 1}^2 \lambda_j(i, g) i_k $.
Electromechanical Force Calculation
Electromechanical force is just the partial derivative of coenergy with respect to mechanical position, the variable $ g $ in this problem.
$ \begin{align} f_e &= \frac{\partial W_c(i_1, i_2, g)}{\partial g} \\ f_e &= N^2 \mu_0 \ell \left(\frac{1}{2} i_1^2 + i_1 i_2 + \frac{1}{2} i_2^2\right) \frac{\partial}{\partial g} G(g) \\ f_e &= N^2 \mu_0 \ell \left(\frac{1}{2} i_1^2 + i_1 i_2 + \frac{1}{2} i_2^2\right) \frac{\partial}{\partial g} \frac{\mu_r w_u d_u}{2 d_s d_u + d_u^2 + w_s w_u + w_u^2 + \mu_r d_u g} \\ f_e &= N^2 \mu_0 \ell \left(\frac{1}{2} i_1^2 + i_1 i_2 + \frac{1}{2} i_2^2\right) \frac{-\mu_r w_u d_u \left(\mu_r d_u\right)}{\left(2 d_s d_u + d_u^2 + w_s w_u + w_u^2 + \mu_r d_u g\right)^2} \end{align} $
Recall by the Quotient Rule or the Chain Rule + Power Rule that $ \frac{d}{dx} \frac{a}{bx + c} = \frac{-ab}{(bx + c)^2} $ for $ a,b,c \in \mathbb{R} $. Thus, the electromechanical force equation is obtained for this device.
$ \begin{equation} \boxed{f_e = -\frac{N^2 \mu_r^2 \mu_0 \ell d_u^2 w_u}{\left(2 d_s d_u + d_u^2 + w_s w_u + w_u^2 + \mu_r d_u g\right)^2} \left(\frac{1}{2} i_1^2 + i_1 i_2 + \frac{1}{2} i_2^2\right)} \end{equation} $