| Line 20: | Line 20: | ||
---- | ---- | ||
---- | ---- | ||
| − | ==Question== | + | ==Question 1== |
[[Image:Q1FO12013.png|Alt text|500x500px]] | [[Image:Q1FO12013.png|Alt text|500x500px]] | ||
| − | [[Image:Q1FO12013D.png|Alt text| | + | [[Image:Q1FO12013D.png|Alt text|200x200px]] |
=Solution= | =Solution= | ||
| + | :'''Click [[ECE_PhD_QE_FO_2013_Problem1.1|here]] to view student [[ECE_PhD_QE_FO_2013_Problem1.1|answers and discussions]]''' | ||
<math> | <math> | ||
\begin{equation*} | \begin{equation*} | ||
| Line 44: | Line 45: | ||
</math> | </math> | ||
| − | ==Question== | + | ==Question 2== |
[[Image:Q2FO12013.png|Alt text|500x500px]] | [[Image:Q2FO12013.png|Alt text|500x500px]] | ||
| Line 52: | Line 53: | ||
<math> | <math> | ||
\begin{align*} | \begin{align*} | ||
| − | \nabla\ | + | \nabla \cdot \bar{D} &= \rho \\ |
\quad (\frac{\partial}{\partial x}\hat{x}+\frac{\partial}{\partial y}\hat{y}+\frac{\partial}{\partial z}\hat{z})\cdot(2\hat{x})&=\rho \\ | \quad (\frac{\partial}{\partial x}\hat{x}+\frac{\partial}{\partial y}\hat{y}+\frac{\partial}{\partial z}\hat{z})\cdot(2\hat{x})&=\rho \\ | ||
\frac{\partial}{\partial x}(2)&=0=\rho \quad \text{(no charge)} | \frac{\partial}{\partial x}(2)&=0=\rho \quad \text{(no charge)} | ||
\end{align*} | \end{align*} | ||
</math> | </math> | ||
| + | |||
| + | Also: | ||
<math> | <math> | ||
| − | |||
\begin{align*} | \begin{align*} | ||
\oint \bar{D}\cdot d\bar{S}&=Q\\ | \oint \bar{D}\cdot d\bar{S}&=Q\\ | ||
| Line 65: | Line 67: | ||
\end{align*} | \end{align*} | ||
</math> | </math> | ||
| + | |||
| + | ==Question 3== | ||
| + | [[Image:Q3FO12013.png|Alt text|500x500px]] | ||
| + | |||
| + | [[Image:Q3FO12013D.png|Alt text|500x500px]] | ||
| + | |||
| + | =Solution= | ||
| + | Using superposition <br/> | ||
| + | In the left cylinder <br/> | ||
| + | <math> | ||
| + | \begin{equation*} | ||
| + | \nabla\times \bar{H}=\bar{J} \longrightarrow \oint \bar{H}\cdot d\bar{l}=\int_S\bar{J}\cdot d\bar{S} | ||
| + | \qquad \left\{ \begin{aligned} | ||
| + | dl&=dr\hat{r}+rd\phi\hat{\phi}+dz\hat{z}\\ | ||
| + | d\bar{S}_z&=rd\phi dr\hat{z} | ||
| + | \end{aligned} \right. | ||
| + | \end{equation*} | ||
| + | </math> | ||
| + | <br/> | ||
| + | <math> | ||
| + | \begin{align*} | ||
| + | \int_0^{2\pi}H_{\phi}(rd\phi)&=\int_0^r\int_0^{2\pi} J_0(r'd\phi dr')\\ | ||
| + | H_{\phi}(2\pi r)&=2\pi J_0(\frac{r^2}{2}) \\ | ||
| + | & \boxed{\bar{H}=\frac{J_0r}{2}\hat{\phi}} | ||
| + | \end{align*} | ||
| + | </math> | ||
| + | <br/> | ||
| + | [[Image:cil.png|Alt text|300x300px]] | ||
| + | <br/> | ||
| + | <math> | ||
| + | \begin{align*} | ||
| + | \text{Transform to cartesian:}&\left\{\begin{aligned} | ||
| + | r&=\sqrt{x^2+y^2}\\ | ||
| + | \hat{\phi}&=-sin\phi\hat{x}+cos\phi\hat{y}\\ | ||
| + | &=(\frac{-y}{\sqrt{x^2+y^2}})\hat{x}+(\frac{x}{\sqrt{x^2+y^2}})\hat{y} | ||
| + | \end{aligned}\right. \\ | ||
| + | & \boxed{\bar{H}_L=\frac{J_0}{2}\left[-y\hat{x}+x\hat{y}\right]} | ||
| + | \end{align*} | ||
| + | </math> | ||
| + | |||
| + | In the right cilinder <br/> | ||
| + | <math> | ||
| + | \begin{align*} | ||
| + | &\bar{H}_R=\frac{-J_0}{2}\left[-y'\hat{x'}+x'\hat{y'}\right]& | ||
| + | \left\{ | ||
| + | \begin{aligned} | ||
| + | x'&=x-3\\ | ||
| + | y'&=y\\ | ||
| + | \hat{x}'&=\hat{x}\\ | ||
| + | \hat{y}'&=\hat{y} | ||
| + | \end{aligned} | ||
| + | \right.\\ | ||
| + | &\boxed{\bar{H}_R=\frac{-J_0}{2}\left[-y\hat{x}+(x-3)\hat{y}\right]}& | ||
| + | \end{align*} | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \begin{equation*} | ||
| + | \boxed{\bar{H}_T=\bar{H}_L+\bar{H}_R=\frac{3J_0}{2}\hat{y}} | ||
| + | \end{equation*} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | |||
Revision as of 21:50, 24 April 2017
Fields and Optics (FO)
Question 1: Statics 1
August 2013
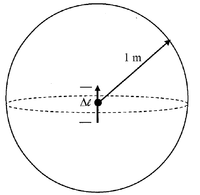
Question 1
Solution
- Click here to view student answers and discussions
$ \begin{equation*} \left.\begin{aligned} \nabla\cdot \bar{B}&=0\\ \oint_S \bar{B}\cdot d\bar{S}&=0 \end{aligned}\right\} \longrightarrow \Phi=\oint_S \bar{B}\cdot d\bar{S} \Longrightarrow \boxed{ \Phi=\oint_S \bar{B}\cdot d\bar{S}=0} \end{equation*} $
The magnetic flux through this closed surface is $ \Phi $
$ \begin{equation*} \boxed{\Phi=0} \end{equation*} $
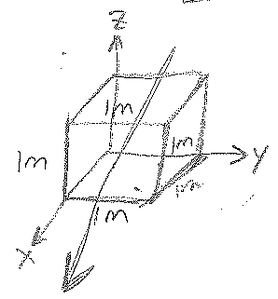
Question 2
Solution
$ \begin{align*} \nabla \cdot \bar{D} &= \rho \\ \quad (\frac{\partial}{\partial x}\hat{x}+\frac{\partial}{\partial y}\hat{y}+\frac{\partial}{\partial z}\hat{z})\cdot(2\hat{x})&=\rho \\ \frac{\partial}{\partial x}(2)&=0=\rho \quad \text{(no charge)} \end{align*} $
Also:
$ \begin{align*} \oint \bar{D}\cdot d\bar{S}&=Q\\ &=\int2(dS_x)+\int2(-dS_x)=2-2=\boxed{0} \end{align*} $
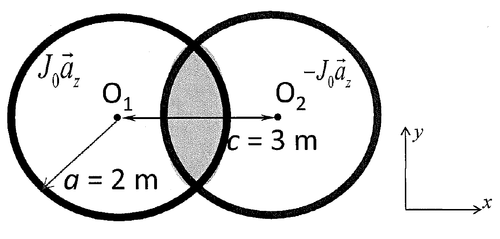
Question 3
Solution
Using superposition
In the left cylinder
$ \begin{equation*} \nabla\times \bar{H}=\bar{J} \longrightarrow \oint \bar{H}\cdot d\bar{l}=\int_S\bar{J}\cdot d\bar{S} \qquad \left\{ \begin{aligned} dl&=dr\hat{r}+rd\phi\hat{\phi}+dz\hat{z}\\ d\bar{S}_z&=rd\phi dr\hat{z} \end{aligned} \right. \end{equation*} $
$ \begin{align*} \int_0^{2\pi}H_{\phi}(rd\phi)&=\int_0^r\int_0^{2\pi} J_0(r'd\phi dr')\\ H_{\phi}(2\pi r)&=2\pi J_0(\frac{r^2}{2}) \\ & \boxed{\bar{H}=\frac{J_0r}{2}\hat{\phi}} \end{align*} $
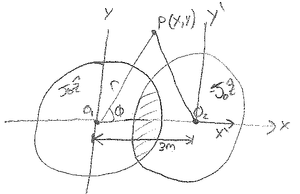
$ \begin{align*} \text{Transform to cartesian:}&\left\{\begin{aligned} r&=\sqrt{x^2+y^2}\\ \hat{\phi}&=-sin\phi\hat{x}+cos\phi\hat{y}\\ &=(\frac{-y}{\sqrt{x^2+y^2}})\hat{x}+(\frac{x}{\sqrt{x^2+y^2}})\hat{y} \end{aligned}\right. \\ & \boxed{\bar{H}_L=\frac{J_0}{2}\left[-y\hat{x}+x\hat{y}\right]} \end{align*} $
In the right cilinder
$ \begin{align*} &\bar{H}_R=\frac{-J_0}{2}\left[-y'\hat{x'}+x'\hat{y'}\right]& \left\{ \begin{aligned} x'&=x-3\\ y'&=y\\ \hat{x}'&=\hat{x}\\ \hat{y}'&=\hat{y} \end{aligned} \right.\\ &\boxed{\bar{H}_R=\frac{-J_0}{2}\left[-y\hat{x}+(x-3)\hat{y}\right]}& \end{align*} $
$ \begin{equation*} \boxed{\bar{H}_T=\bar{H}_L+\bar{H}_R=\frac{3J_0}{2}\hat{y}} \end{equation*} $
Question
Part 1.
Consider $ n $ independent flips of a coin having probability $ p $ of landing on heads. Say that a changeover occurs whenever an outcome differs from the one preceding it. For instance, if $ n=5 $ and the sequence $ HHTHT $ is observed, then there are 3 changeovers. Find the expected number of changeovers for $ n $ flips. Hint: Express the number of changeovers as a sum of Bernoulli random variables.
- Click here to view student answers and discussions
Part 2.
Let $ X_1,X_2,... $ be a sequence of jointly Gaussian random variables with covariance
$ Cov(X_i,X_j) = \left\{ \begin{array}{ll} {\sigma}^2, & i=j\\ \rho{\sigma}^2, & |i-j|=1\\ 0, & otherwise \end{array} \right. $
Suppose we take 2 consecutive samples from this sequence to form a vector $ X $, which is then linearly transformed to form a 2-dimensional random vector $ Y=AX $. Find a matrix $ A $ so that the components of $ Y $ are independent random variables You must justify your answer.
- Click here to view student answers and discussions
Part 3.
Let $ X $ be an exponential random variable with parameter $ \lambda $, so that $ f_X(x)=\lambda{exp}(-\lambda{x})u(x) $. Find the variance of $ X $. You must show all of your work.
- Click here to view student answers and discussions
Part 4.
Consider a sequence of independent random variables $ X_1,X_2,... $, where $ X_n $ has pdf
$ \begin{align}f_n(x)=&(1-\frac{1}{n})\frac{1}{\sqrt{2\pi}\sigma}exp[-\frac{1}{2\sigma^2}(x-\frac{n-1}{n}\sigma)^2]\\ &+\frac{1}{n}\sigma exp(-\sigma x)u(x)\end{align} $.
Does this sequence converge in the mean-square sense? Hint: Use the Cauchy criterion for mean-square convergence, which states that a sequence of random variables $ X_1,X_2,... $ converges in mean-square if and only if $ E[|X_n-X_{n+m}|] \to 0 $ as $ n \to \infty $, for every $ m>0 $.
- Click here to view student answers and discussions