Whitening and Coloring Transforms for Multivariate Gaussian Random Variables
A slecture by ECE student Maliha Hossain
Partly based on the ECE662 Spring 2014 lecture material of Prof. Mireille Boutin.
Contents
Introduction
Data whitening is required prior to many data processing techniques such as principal component analysis, independent component analysis, etc. This slecture discusses how to whiten data that is normally distributed but keep in mind that although I have illustrated the whitening and coloring transforms with Gaussian data, these transforms can be used on data drawn from according to any probability law. The slecture also covers how to transform white data so that it resembles data drawn from another Gaussian distribution with known mean and covariance. This will be useful material for when the reader would like to generate data points from non-white Gaussian distributions.
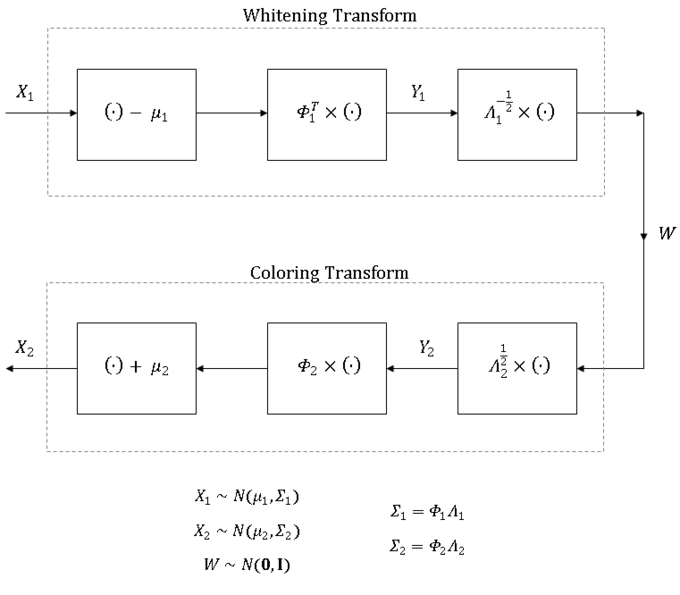
Throughout this slecture, we will denote the probability density function (pdf) of the random variable X as f$ _X $ : R$ ^d $ → R where X ∈ R$ ^d $ is a d-dimensional Gaussian random vector with mean μ and covariance matrix Σ. This slecture assumes that the reader is familiar with topics from linear algebra including but not limited to vector spaces, eigenvalues, and eigenvectors. It is no surprise that eigendecomposition plays an important role in data whitening since we would ultimately like to produce a diagonal covariance matrix. The transforms revolve around expressing Σ as
We will focus on finding U via eigendecomposition but there are other methods such as the Cholesky decomposition for symmetric positive definite matrices that could be used to correlate and decorrelate vectors.
The pdf of X is given by
Whitening Transform
Let X be a multivariate Gaussian random vector with arbitrary covariance matrix Σ and mean vector μ. We would like to transform it to another random vector whose covariance is the identity matrix. This means that the components of our new random variable are uncorrelated and have variance 1. This process is called whitening because the output resembles a white noise vector.
There are two steps to the procedure. First, we must decorrelate the components of the vector. This produces a data point drawn from a distribution with a diagonal covariance matrix. Finally, we must scale the different components so that they have unit variance. In order to do this, we need the eigendecomposition of the original covariance matrix Σ. This is either known or it can be estimated from your data set. We assume that Σ is positive definite. We also assume wlog that X has zero mean. If not, then subtract the mean (estimated or otherwise) from your samples such that
The covariance matrix can be expressed as follows
where Λ is a diagonal matrix with the eigenvalues, λ$ _i $, of Σ on the diagonal and Φ is the matrix of corresponding eigenvectors, e$ _i $. In addition, the columns of Φ are orthonormal so that
Let
Then Y is a random vector with a decorrelated multivariates Gaussian distribution with variances λ$ _i $ on the diagonal of its covariance matrix. The next step then is quite obvious. Let
W is then random vector with the standard multivariate distribution. Note that X = x, Y = y, and W = w are at the same Mahalanobis distance away from their respective means (in this case, the origin) and in the case of W, the Mahalanobis distance and the Euclidean distance are the same.
Now that you have the procedure, you may be asking why this transform works. Well, we can derive the covariance matrix of Y. Recall that its mean is the zero vector so its covariance is
This proves what we previously stated; the components of Y are uncorrelated since the covariance matrix is diagonal. In the Gaussian case, this is equivalent to independence since we can express the joint pdf of the components of Y as a product of the marginals.
Using the fact that diagonal matrix Λ$ ^{0.5} $ is symmetric, the covariance matrix of W is
This concludes the proof of how the linear transform given by matrix pre-multiplication by Λ$ ^{-0.5} $Φ$ ^T $ produces whitened data.
Let us now work through an example. For the purpose of illustration, I will use a bivariate Gaussian vector X∼N(0,Σ) where
Let S be the collection of data points obtained by taking $ n $ samples from X. The columns of S are random vectors X$ _i $, $ i = 1,2,...,n $. S can be generated in MATLAB using the following code.
% Generate n samples from colored bivariate Gaussian n = 1000; CovX = [10 -6;-6 5]; mu = [0 0]; S = mvnrnd(mu,CovX,n); S = S';
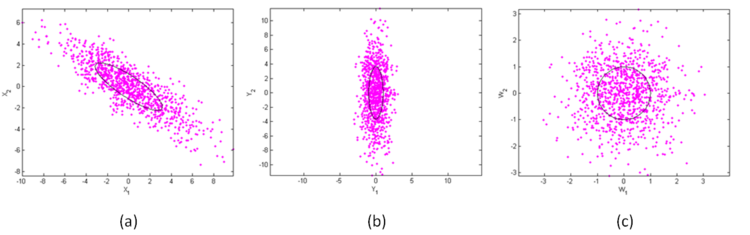
Figure 1(a) shows a scatter plot of the generated samples along with one contour at unit Mahalanobis distance. The contour is an ellipse that is centered at the origin and rotated through an angle. Say that we do not know the parameters of the distribution from which S was obtained so we estimate them. We use the maximum likelihood estimates for the parameters.
The code for the above estimation is given by
% sample mean mus = mean(S,2); % estimate covariance Covs = bsxfun(@minus,S,mus) * bsxfun(@minus,S,mus)'/(n-1);
Next, we find the eigenvectors of the estimated covariance matrix by finding the orthonormal basis for the nullspace of matrix (Σ-λ$ _i $I). In MATLAB, we simply use the eig command to find both Φ and Λ.
[Phi,Lam] = eig(Covs);
Now let
Then, Y is a set of $ n $ data points drawn from an uncorrelated bivariate Gaussian distribution with diagonal covariance matrix Λ. The premultiplication by Φ essentially rotates the ellipse in figure 1(a) so that its principal axes are aligned with the $ x_1-x_2 $ axes. The result of this transformation is shown in figure 1(b).
Finally, we scale the samples so the radii of the ellipse are of unit length.
In MATLAB,
W = sqrt(Lam)\ Y;
The whitened data is shown in figure 1(c). Note that the normalization produces a contour that is now a circle. From MATLAB, the estimated covariance of the whitened samples is given by
Note that the whitening transform is not unique. If e$ _1 $ is an eigenvector, then so is -e$ _1 $. Also, Λ$ ^{-0.5} $ is not unique either. We could have taken the negative roots of the eigenvalues but since we think of them as standard deviations, it is easier to think of them as positive quantities. In our intermediary step, we rotated the ellipse so that the major axis is aligned vertically in figure 1(c) but we could have done it the other way around and arrived at the same conclusion.
Coloring Transform
The coloring transform is the inverse of the whitening transform. Here we see how to transform W, a multivariate Gaussian variable whose components are i.i.d with unit variance to X, a Gaussian random vector with some desired covariance matrix.
Say you have S, a matrix whose $ n $ columns are $ n $ samples drawn from a whitened Gaussian distribution. So S is of the form [W$ _1 $,...W$ _n $] but what you want is $ n $ samples from a distribution that has covariance matrix Σ and mean μ. The first step is to perform the eigendocomposition of your desired covariance matrix Σ.
where Λ is a diagonal matrix with the eigenvalues, λ$ _i $, of Σ on the diagonal and Φ is the matrix of corresponding eigenvectors, e$ _i $. In addition, the columns of Φ are orthonormal so that
The first step is to scale the samples so their spread reflects your desired variances along the principal axes. This step changes the spherical contours to elliptical ones.
The next step is to rotate the data points so that they are now correlated.
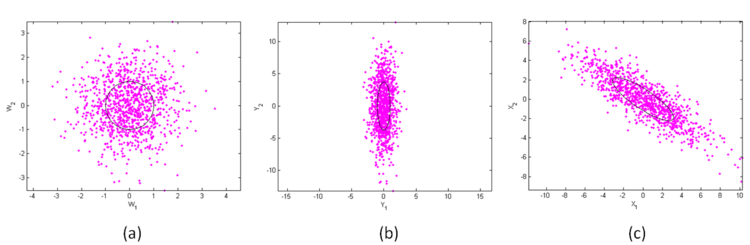
Figure 2 shows the mapping from W to Y to X for a bivariate distribution with
It is just like figure 1 from right to left. Just like the whitening transform, the coloring transform is not unique either. Finally, add μ to your samples so that the mean is translated from the origin to your desired location. The transform can be implemented in MATLAB with the following code.
function[X] = colortran(mu, CovX, N) % function generates N data points from multivariate Gaussian % with mean vector mu and covariance matrix CovX. % Find eigenvectors and eigenvalues [Phi,Lam] = eig(CovX); % Generate N samples of white data d = length(mu); S = mvnrnd(zeros(1,d),eye(d),N)'; % Scale to desired variances Y = sqrt(Lam)*S; % Rotate or correlate samples X = Phi*Y; % Add the mean vector to every column of X X = bsxfun(@plus,X,mu); end
Summary
So we see that data whitening can be broken down into two steps:
- Decorrelation. In other words, a rotation that maps the data so that the axes along which the original data has the largest variance are aligned with your co-ordinate axes. The resulting covariance matrix is diagonal. This is really just a change of basis.
- Scaling so that the principal axes are each of unit length. The data is squeezed or stretched along individual axes depending on whether the variance along said axis is greater or less than one. The resulting covariance matrix is identity.
We can summarize coloring as the inverse of whitening. I also find it helpful to compare it with the simplest case, when we are working with scalars. Recall that multiplying a random variable with a constant produces another whose standard deviation is scaled by a factor equal to said constant. Consequently, If $ W $ is a random variable of unit variance and $ X = c.W $, then $ X $ has standard deviation $ c.1 $ and variance $ c^2 $. This multiplication is a linear transform. In the multivariate case, we are expressing our desired covariance matrix as a product
where U$ ^T $ = ΦΛ$ ^{0.5} $. This U$ ^T $ is our linear transform and is analogous to $ c $ in the scalar case.
I am aware that MATLAB comes with the mvnrnd command that can generate data points from any multivariate Gaussian distribution but hopefully, this material provides sufficient background to allow the reader to not only whiten and color data but also to transform data from one distribution to another in other programs that are not equipped with the same out of the box capabilities as MATLAB. A summary of this process is presented in figure 3.
References
[1]. Charles A. Bouman, Digital Image Processing Laboratory: Eigen-decomposition of Images. February 22, 2013
[2]. Mireille Boutin, "ECE662: Statistical Pattern Recognition and Decision Making Processes," Purdue University, Spring 2014.
[3]. Gilbert Strang, Linear Algebra and its Applications. Thomson Brooks/Cole. 4th Edition, 2006.
Questions and comments
If you have any questions, comments, etc. please post them on this page.