Question
There is a stick of length 1. We break it at a random spot and take the leftmost part as a stick of length x. Then we break THAT stick at a random spot and take the leftmost part as a stick of length y. Find the PDF of Y.
Answer
f(x) = 1 for 0 < x < 1
f(x) = 0 otherwise
We also know that
fY|X(y|x) = 1/x for 0 < y < x
fY|X(y|x) = 0 otherwise
This is the graph of fY|X(y|x):
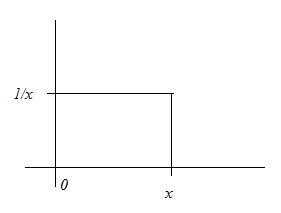
Using the theorem of total probability for continuous RVs, we have that
$ f_{Y}(y) = \int_{-\infty}^{\infty}f_{Y|X}(y|x)f_{X}(x) dx $
$ = \int_{0}^{1}f_{Y|X}(y|x)(1) dx $
because we are doing an integral of x, and the probability that x < y or x > 1 is 0, the limits of integration become from y to 1:
$ = \int_{y}^{1}\frac{1}{x} dx $
$ = ln(\frac{1}{y}), 0 < y < 1 $