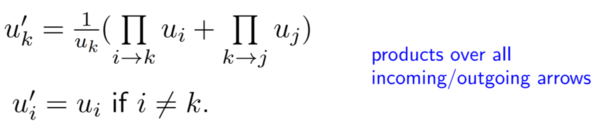Mutations Revisited
Now that we have gotten some basic ideas of algebra out of the way, we can return focus to cluster algebra, in particular. As the basic idea behind cluster algebra is recursively constructing a ring from an initial set of variables (the initial seed), it would be helpful to find some way of visualizing this --- it just so happens that quiver mutations are the perfect tool to do this.
Imagine an initial seed (u, Q), consisting of an arbitrary quiver, Q, with vertices labeled by the set of variables u = {u1, u2, …, un}. If we apply a quiver mutation to Q, then a new quiver will be formed along with new vertex labels, which is the seed (u’, Q’). We already know how to draw this new graph, but what about the labeling of these new vertices? The part of a “cluster algebra” that makes it unique is how its elements are generated, which is referred to as the “exchange relation” and is precisely given by the formula below from [3]:
Essentially, if we perform a mutation on a vertex k, the new seed that we create will consist of the exact same vertex labeling, except for the replacement of uk with uk’, given by the formula above --- this particular construction of new rational expressions is the unique part of cluster algebra.
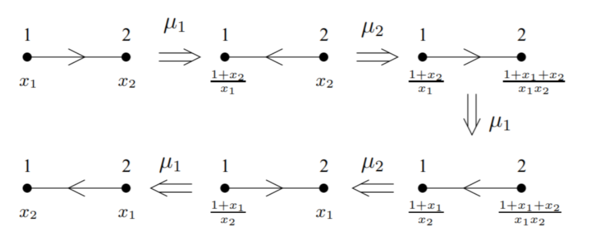
To help make this concept more clear, the following diagram from Figure 1 of [2] outlines a possible sequence of mutations on the quiver Q1 of a single directed edge. Note: the initial seed in this diagram is given by ({x1, x2}, Q1), with mutations denoted by μn, which is a slightly different notation than above.
Note: all bullet points above were written by me.