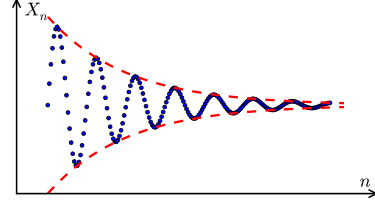
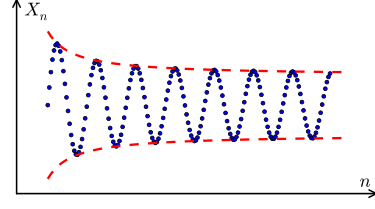
Cauchy Sequences:
A cauchy sequence is a sequence whose terms converge to being arbitrarily close to each other over time. For example, a sequence defined by xn within a normed space is a Cauchy Sequence if and only if:
Given ε > 0, there exists N such that: if m, n > N then |am- an| < ε
Essentially, over time, given ε, an arbitrarily small positive distance, the terms of said sequence xn become at most ε apart from each other.
In the above visual, the blue represents the terms of xn over n iterations. As the definition in itself is a bit vague as far as what an “arbitrarily small distance” is, the important thing to note is the general reduction in the distance between the elements of the series as well as the gradual convergence of the resulting distances between each term. However a sequence that follows the model:
would not be defined as Cauchy due to the fact that over time(n), the terms do not approach the defined arbitrarily small positive value, keeping their distance from each other.
Cauchy Sequences and Completeness: Given some vector space X, the vector space is complete if, “every Cauchy sequence in X converges” (sec3.1.pdf).