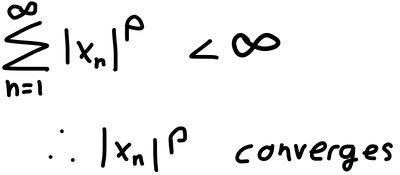Banach Spaces:
A Banach Space is defined as a “complete normed linear vector space” (sec3.1.pdf) by Purdue Math. Using the definitions previously discussed in this essay, a Banach Space is the pairing of some vector field X and some norm ||.||, commonly denoted by (X, ||.||).
Definition 1:
A metric is a distance function that defines the difference between two points in any given set. The associated metric to a norm is given as d(||.||)(x, y) = |y - x| where ||.|| is a given norm, representing the normal metric of real numbers.
Using definition 1, it becomes a little more clear what the use of a Banach Space is. It essentially links a metric with a real or complex vector space through the use of a norm. This allows for complex analysis of a vector space through the use of scalars.
Banach Spaces In 1 Dimension:
Given that vector field R, is a one dimensional, real vector space:
R from [0, ∞) is a norm (||.||).
d(||.||)(x, y) = ||y - x|| is the associated metric.
Thus, the Banach Space is defined as (R, ||.||).
Banach Spaces In p Dimensions:
As you get into further dimensions of Banach Spaces, they become almost comically complex. The definition is as follows:
Let |N = all natural numbers and let |F = the field (the set of complex or real numbers).
Given (xn ∈ |N), Let some set Lp(|N, |F) = all sequences in |F and in |N converge for:
Thus, the resulting Banach Space in p dimensions is denoted by (Lp, ||.||p).