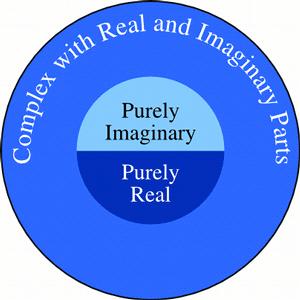
To start off click on the link below to see a diagram of how signals are organized into complex, real, imaginary, or both. Notice that all real, imaginary, and neither real nor imaginary signals are complex
- Complex
- A complex signal x(t) can be written in the form x(t) = a(t) + \jmath b(t), where a(t) and b(t) are real signals
- Real
- A real signal is a complex signal x(t) = a(t) + jb(t) where b(t) = 0
- Imaginary
- A (pure) imaginary signal is a complex signal x(t) = a(t) + jb(t) where a(t) = 0
Examples
- Complex, but not purely real nor imaginary
- x(t) = 3t + jt
- Real
- x(t) = 3t
- Imaginary
- x(t) = jt
- Both Real and Imaginary
- x(t) = 0, Because x(t) = 0 can be rewritten as x(t) = 0 + j0
Practice
Is $ x(t) = \sum_{k=0}^7 \sin{k\pi t} $ real, imaginary, or complex? List all correct answers Solution: If you look at, for example, the k=1 term, x1(t) = sin((pi)t) This signal can be rewritten in the form of x(t) = a(t) + jb(t) So x1(t) = sin((pi)t) + j0 Therefore the imaginary part of the signal is zero and the real part is a function of t, and this signal be written in the complex form, so it must be complex as well
And since x(t) can be written as the sum of these sine functions, x(t) can be written in the form x(t) = a(t) + jb(t) Where a(t) is going to be the entire sum, and b(t) will be zero
Therefore this sum is real and complex, but not imaginary
Is x(t) = exp(j(pi)t)*[cos((pi)t) - jsin((pi)t)]? real, imaginary, or complex? List all correct answers Solution: Since exp(j(pi)t) = cos((pi)t) + jsin((pi)t)
The entire equation is simplified to x(t) = (cos((pi)t))^2 + (sin((pi)t))^2 This is simplified to x(t) = 1, which can be written as x(t) = 1 + j0
Therefore x(t) is real and complex, but not imaginary