Page 6 - Rhea

Bernoulli Trials and Binomial Distribution

Thus far, we have observed how $ e $ relates to compound interest and its unique properties involving Euler's Formula and the imaginary number $ i $. In this section, we will take a look at a potentially mysterious instance of how $ e $ appears when working with probability and will attempt to discover some explanations of why this occurs at all. Before we do this, however, let us begin with a few definitions.

Bernoulli Trial
Earlier in the text, we briefly learned of Jacob Bernoulli and relating $ e $ to compound interest using the limit definition $ e=\lim_{n \to \infty}\left(1+\frac1n\right)^n $. We will now observe more of Bernoulli's work in the form of the Bernoulli Trial.

A Bernoulli Trial is a discrete experiment with two possible outcomes, described as "success" or "failure" of some event $ E $. In each trial, the event $ E $ has a constant probability $ p $ of occurring. Therefore, with one trial, the probability of the event occurring once is $ P(1)=p $, and the probability of the event occurring zero times is $ P(0)=1-p $.

Binomial Distribution
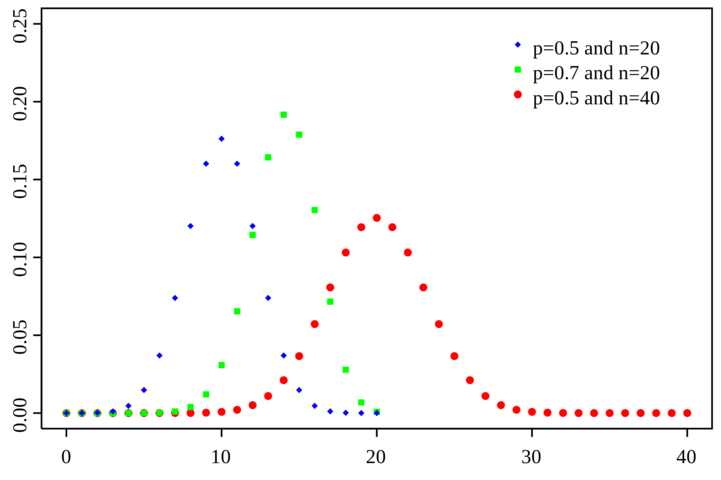
A Binomial Distribution involves repeating a Bernoulli Trial some number of times, $ n $, each with the same probability $ p $. As such, the binomial distribution depends on both $ n $ and $ p $. An example distribution with varying values for $ n $ and $ p $ is shown in the image below^[1].

As seen in this image, the overall range of values depends solely on $ n $ as, with $ n $ trials, the event can only occur $ 0 $ to $ n $ times. The peak of the distribution, however, occurs at $ np $, and the overall range set by $ n $ will affect how centralized the distribution is, with smaller ranges resulting in less variance and larger ranges resulting in greater variance.

Finally, let us consider the probability that the event occurs some number of times, $ i $. We have already stated that, for each individual trial, the probability of the event occurring is $ p $. For multiple trials, however, the event must occur $ i $ times, each with probability p, and the event will not occur the remaining $ n-i $ times, each with probability $ 1-p $. These $ i $ successes, however, can occur in $ {n \choose i} $ different ways. Therefore, the probability of the event occurring $ i $ times can be found using the following formula^[2]:

$ \begin{align} P(i)=p^i(1-p)^{n-i}{n \choose i}=p^i(1-p)^{n-i}\frac{n!}{i!(n-i)!} \end{align} $

where $ P(i) $ denotes the probability of the event occurring $ i $ times after $ n $ trials, each with probability $ p $.

$ e $ in Binomial Distribution

So what does all of this have to do with $ e $? Well, in order to determine that, let us consider the following example.

Suppose you are playing a game in which you roll a six-sided die, and you "lose" if you ever roll a $ 1 $. If you roll the die six times, what is the probability that you will "win" this game by not rolling a single $ 1 $?

Well, for each roll, there is a $ \frac{1}{6} $ chance that you will roll a $ 1 $, so you have a $ \frac{5}{6} $ chance of not rolling a $ 1 $ for any individual roll. Therefore, the probability of not rolling a $ 1 $ on any of the six rolls is $ (\frac{5}{6})^6\approx0.334898 $.

Now, let us increase the value, which we will now call $ n $, from six to twenty. The probability of not rolling a $ 1 $ on a twenty-sided die is $ \frac{19}{20} $, so the probability of never rolling a $ 1 $ after twenty rolls is $ (\frac{19}{20})^20\approx0.358486 $.

Lucky for you, the odds have increased, so you may suddenly be wondering how high can they get? If increasing $ n $ from six to twenty improved your odds from $ 33.5% $ to $ 35.8% $, what happens if we continue to increase $ n $ to even larger values? The table below shows the probability of never rolling a one for various values of $ n $.

$ \begin{array}{|c|c|}\hline n & P(0)\\\hline 6 & 0.334898\\\hline 20 & 0.358486\\\hline 100 & 0.366032\\\hline 100,000 & 0.367878\\\hline 1,000,000 & 0.367879\\\hline \end{array} $

As can be seen from the table, the value of the formula seems to approach some number, approximately $ 0.367879 $. To find an exact value, let us extract a limit to describe the formula of $ P(0) $ using a substituted variable $ m=n-1 $:

$ \begin{align}P(0) &=\lim_{n\to\infty}(\frac{n-1}{n})^n\\ &=\lim_{m\to\infty}(\frac{m}{m+1})^{m+1}\\ &=\lim_{m\to\infty}(\frac{m}{m+1})*\lim_{m\to\infty}(\frac{m}{m+1})^{m}\\ &=\lim_{m\to\infty}(\frac{m+1}{m})^{-m}\\ &=\lim_{m\to\infty}(1+\frac{1}{m})^{-m}\ \end{align} $

Now you may recognize this formula as the reciprocal of Bernoulli's definition of $ e $ stated earlier in the text. Therefore, it can be determined that the probability of not rolling a single $ 1 $ after rolling an $ N- $sided die $ N $ times becomes $ \frac{1}{e} $ as $ N $ approaches $ \infty $.

In fact, this holds true for the general form as well. For any event with a $ \frac{1}{N} $ probability of occurring, after $ N $ trials, there will be a $ \frac{1}{e} $ probability that it never occurs. This can be confirmed using the formula for $ P(i) $ which we found earlier in the section. Let $ i=0 $ and $ p=\frac{1}{n} $.

$ \begin{align}P(0) &=\lim_{n\to\infty}(\frac{1}{n})^0(1-\frac{1}{n})^n\frac{n!}{0!(n-0)!}\\ &=\lim_{n\to\infty}(1-\frac{1}{n})^n\frac{n!}{n!}\\ &=\lim_{n\to\infty}(1-\frac{1}{n})^n\\ &=e^{-1} \end{align} $

So we have now seen one instance of how $ e $ shows up in relatively unexpected places due to its unique properties. It can be quite fascinating how integer repetition of experiments with rational probabilities seems to suddenly yield a very specific transcendental number, $ e $.

References

Probability mass function for the binomial distribution [Digital image]. (2008, March 2). Retrieved December 1, 2018, from https://en.wikipedia.org/wiki/Binomial_distribution#/media/File:Binomial_distribution_pmf.svg

Weisstein, E. W. (n.d.). Binomial Distribution. MathWorld--A Wolfram Web Resource. Retrieved December 1, 2018, from http://mathworld.wolfram.com/BinomialDistribution.html

Back to Mysteries of the Number e